2.10 Consistent Covariance Matrix Estimation
Consider again the regression model in Eq. (2.43). There may exist situations in which the error term et has serial correlations and/or conditional heteroscedasticity, but the main objective of the analysis is to make inference concerning the regression coefficients α and β. See Chapter 3 for discussion of conditional heteroscedasticity. In situations under which the OLS estimates of the coefficients remain consistent, methods are available to provide consistent estimate of the covariance matrix of the coefficient estimates. Two such methods are widely used. The first method is called the heteroscedasticity consistent (HC) estimator; see Eicker (1967) and White (1980). The second method is called the heteroscedasticity and autocorrelation consistent (HAC) estimator; see Newey and West (1987).
For ease in discussion, we shall rewrite the regression model as
where yt is the dependent variable, 
is a k-dimensional vector of explanatory variables including constant, and 
is the parameter vector. Here 
denotes the transpose of the vector 
. The LS estimate of 
and the associate covariance matrix are
where 
is the variance of et and is estimated by the variance of the residuals of the regression. In the presence of serial correlations or conditional heteroscedasticity, the prior covariance matrix estimator is inconsistent, often resulting in inflating the t ratios of 
.
The estimator of White (1980) is
where 
is the residual at time t. The estimator of Newey and West (1987) is
2.50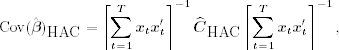 
where
where ℓ is a truncation parameter and wj is a weight function such as the Bartlett weight function defined by
Other weight functions can also be used. Newey and West (1987) suggest choosing ℓ to be the integer part of 4(T/100)2/9. This estimator essentially uses a nonparametric method to estimate the covariance matrix of 
.
For illustration, we employ the first differenced interest rate series in Eq. (2.45). The t ratio of the coefficient of c1t is 107.91 if both serial correlation and heteroscedasticity in the residuals are ignored, it becomes 48.44 when the HC estimator is used, and it reduces to 39.92 when the HAC estimator is used. The S-Plus demonstration below also uses a regression that includes lagged values c1, t−1 and c3, t−1 as regressors to take care of serial correlations in the residuals. One can also apply the HC or HAC estimator to the fitted model to refine the t ratios of the coefficient estimates.
S-Plus Demonstration
The following output has been edited and % denotes explanation:
> module(finmetrics)
> r1=read.table(“w-gs1yr.txt”,header=T)[,4] % Load data
> r3=read.table(“w-gs3yr.txt”,header=T)[,4]
> c1=diff(r1) % Take 1st difference
> c3=diff(r3)
> reg.fit=OLS(c3 ˜ c1) % Fit a simple linear regression.
> summary(reg.fit)
Call:
OLS(formula = c3 ˜ c1)
Residuals:
Min 1Q Median 3Q Max
-0.4246 -0.0358 -0.0012 0.0347 0.4892
Coefficients:
Value Std. Error t value Pr(>|t|)
(Intercept) -0.0001 0.0014 -0.0757 0.9397
c1 0.7919 0.0073 107.9063 0.0000
Regression Diagnostics:
R-Squared 0.8253
Adjusted R-Squared 0.8253
Durbin-Watson Stat 1.6456
Residual Diagnostics:
Stat P-Value
Jarque-Bera 1644.6146 0.0000
Ljung-Box 230.0477 0.0000
Residual standard error: 0.06897 on 2464 degrees of freedom
> summary(reg.fit,correction=“white”) % Use HC the estimator
Coefficients:
Value Std. Error t value Pr(>|t|)
(Intercept) -0.0001 0.0014 -0.0757 0.9396
c1 0.7919 0.0163 48.4405 0.0000
> summary(reg.fit,correction=“nw”) % Use the HAC estimator
Coefficients:
Value Std. Error t value Pr(>|t|)
(Intercept) -0.0001 0.0016 -0.0678 0.9459
c1 0.7919 0.0198 39.9223 0.0000
% Below, fit a regression model with time series errors.
> reg.ts=OLS(c3 ˜ c1+tslag(c3,1)+tslag(c1,1),na.rm=T)
> summary(reg.ts)
Call:
OLS(formula = c3 ˜ c1 + tslag(c3, 1)+tslag(c1, 1), na.rm = T)
Residuals:
Min 1Q Median 3Q Max
-0.4481 -0.0355 -0.0008 0.0341 0.4582
Coefficients:
Value Std. Error t value Pr(>|t|)
(Intercept) -0.0001 0.0014 -0.0636 0.9493
c1 0.7971 0.0077 103.6320 0.0000
tslag(c3, 1) 0.1766 0.0198 8.9057 0.0000
tslag(c1, 1) -0.1580 0.0174 -9.0583 0.0000
Regression Diagnostics:
R-Squared 0.8312
Adjusted R-Squared 0.8310
Durbin-Watson Stat 1.9865
Residual Diagnostics:
Stat P-Value
Jarque-Bera 1620.5090 0.0000
Ljung-Box 131.6048 0.0000
Residual standard error: 0.06785 on 2461 degrees of freedom
Let 
be the jth element of 
. When k > 1, the HC variance of 
in Eq. (2.49) can be obtained by using an auxiliary regression. Let 
be the (k − 1)-dimensional vector obtained by removing the element xjt from 
. Consider the auxiliary regression
2.51 
Let 
be the least-squares residual of this auxiliary regression. It can be shown that
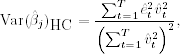
where êt is the residual of original regression in Eq. (2.48). The auxiliary regression is simply a step taken to achieve orthogonality between 
and the rest of the regressors so that the formula in Eq. (2.49) can be simplified.