Quantile estimation provides a nonparametric approach to VaR calculation. It makes no specific distributional assumption on the return of a portfolio except that the distribution continues to hold within the prediction period. There are two types of quantile methods. The first method is to use empirical quantile directly, and the second method uses quantile regression.
7.4.1 Quantile and Order Statistics
Assuming that the distribution of return in the prediction period is the same as that in the sample period, one can use the empirical quantile of the return rt to calculate VaR. Let r1, … , rn be the returns of a portfolio in the sample period. The order statistics of the sample are these values arranged in increasing order. We use the notation
to denote the arrangement and refer to r(i) as the ith order statistic of the sample. In particular, r(1) is the sample minimum and r(n) the sample maximum.
Assume that the returns are independent and identically distributed random variables that have a continuous distribution with probability density function (pdf) f(x) and CDF F(x). Then we have the following asymptotic result from the statistical literature [e.g., Cox and Hinkley (1974), Appendix 2], for the order statistic r(ℓ), where ℓ = np with 0 < p < 1.
Result
Let xp be the pth quantile of F(x), that is, xp = F−1(p). Assume that the pdf f(x) is not zero at xp [i.e., f(xp) ≠ 0]. Then the order statistic r(ℓ) is asymptotically normal with mean xp and variance p(1 − p)/[nf2(xp)]. That is,
7.11 
Based on the prior result, one can use r(ℓ) to estimate the quantile xp, where ℓ = np. In practice, the probability of interest p may not satisfy that np is a positive integer. In this case, one can use simple interpolation to obtain quantile estimates. More specifically, for noninteger np, let ℓ1 and ℓ2 be the two neighboring positive integers such that ℓ1 < np < ℓ2. Define pi = ℓi/n. The previous result shows that 
is a consistent estimate of the quantile 
. From the definition, p1 < p < p2. Therefore, the quantile xp can be estimated by
7.12 
In practice, sample quantiles can easily be obtained from most statistical packages, including R and S-Plus. A demonstration is given after the examples.
Example 7.4
Consider the daily log returns of Intel stock from December 15, 1972, to December 31, 2008. There are 9096 observations. For a long position in the Intel stock, we consider the negative log returns. Since 9096 × 0.95 = 8641.2, we have ℓ1 = 8641, ℓ2 = 8642, p1 = 8641/9096, and p2 = 8642/9096. The empirical 95% quantile of the negative log returns can be obtained as
r(i) is the ith order statistic of the negative log returns. In this particular instance, r(8641) = 4.2951% and r(8642) = 4.2954%.
7.4.1.1 R Demonstration
> da=read.table(“d-intc7208.txt”,header=T)
> intc=log(da[,2]+1)
> nintc=-intc
> quantile(nintc,0.95)
95%
0.04295213
> quantile(rtn,.05) % An alternative
5%
−0.04295213
Example 7.5
Consider again the daily log returns of IBM stock from July 3, 1962, to December 31, 1998. Using all 9190 observations, the empirical 95% quantile of the negative log returns can be obtained as (r(8730) + r(8731))/2 = 0.021603, where r(i) is the ith order statistic and np = 9190 × 0.95 = 8730.5. The VaR of a long position of $10 million is $216, 030, which is much smaller than those obtained by the econometric approach discussed before. Because the sample size is 9190, we have 9098 < 9190 × 0.99 < 9099. Let p1 = 9198/9190 = 0.98999 and p2 = 9099/9190 = 0.9901. The empirical 99% quantile can be obtained as
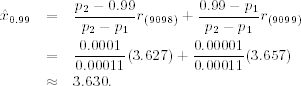
The 1% 1-day horizon VaR of the long position is $363, 000. Again this amount is lower than those obtained before by other methods.
Advantages of using the empirical quantile method to VaR calculation include (a) simplicity and (b) using no specific distributional assumption. However, the approach has several drawbacks. First, it assumes that the distribution of the return rt remains unchanged from the sample period to the prediction period. Given that VaR is concerned mainly with tail probability, this assumption implies that the predicted loss cannot be greater than that of the historical loss. It is definitely not so in practice. Second, when the tail probability p is small, the empirical quantile is not an efficient estimate of the theoretical quantile. Third, the direct quantile estimation fails to take into account the effect of explanatory variables that are relevant to the portfolio under study. In real application, VaR obtained by the empirical quantile can serve as a lower bound for the actual VaR.
The expected shortfall can also be estimated directly from the sample returns. Let 
be the empirical qth quantile, where q = 1 − p with p being the upper tail probability. We have
where I[ · ] = 1 if 
and = 0, otherwise, and Nq denotes the number of xi greater than 
. For illustration, consider the negative IBM daily log returns. If p = 0.01, we have 
. Therefore, ES0.99 = 5.097.
7.4.1.2 R Demonstration
> da=read.table(”d-ibm6298.txt”,header=T)
> ibm=log(da[,2]+1)*100
> nibm=-ibm
> q99=quantile(nibm,0.99)
> q99
99%
[1] 3.630295
> idx=c(1:length(nibm))[nibm>q99] % locate the exceedances
> es=mean(nibm[idx])
> es
[1] 5.097222
7.4.2 Quantile Regression
In real application, one often has explanatory variables available that are important to the problem under study. For example, the action taken by Federal Reserve Banks on interest rates could have important impacts on the returns of U.S. stocks. It is then more appropriate to consider the distribution function rt+1|Ft, where Ft includes the explanatory variables. In other words, we are interested in the quantiles of the distribution function of rt+1 given Ft. Such a quantile is referred to as a regression quantile in the literature; see Koenker and Bassett (1978).
To understand regression quantile, it is helpful to cast the empirical quantile of the previous subsection as an estimation problem. For a given probability p, the pth quantile of {rt} is obtained by
where wp(z) is defined by
Regression quantile is a generalization of such an estimate.
To see the generalization, suppose that we have the linear regression
7.13 
where β is a k-dimensional vector of parameters and 
t is a vector of predictors that are elements of Ft−1. The conditional distribution of rt given Ft−1 is a translation of the distribution of at because 
is known. Viewing the problem this way, Koenker and Bassett (1978) suggest estimating the conditional quantile xp|Ft−1 of rt given Ft−1 as
7.14 
where “
” means that 
is obtained by
where wp( · ) is defined as before. A computer program to obtain such an estimated quantile can be found in Koenker and D'Orey (1987). The package quantreg of R performs quantile regression analysis.