Suppose that there are k assets and T time periods. Let rit be the return of asset i in the time period t. A general form for the factor model is
where αi is a constant representing the intercept, {fjt|j = 1, … , m} are m common factors, βij is the factor loading for asset i on the jth factor, and ϵit is the specific factor of asset i.
For asset returns, the factor 
is assumed to be an m-dimensional stationary process such that
and the asset specific factor ϵit is a white noise series and uncorrelated with the common factors fjt and other specific factors. Specifically, we assume that
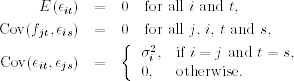
Thus, the common factors are uncorrelated with the specific factors, and the specific factors are uncorrelated among each other. The common factors, however, need not be uncorrelated with each other in some factor models.
In some applications, the number of assets k may be larger than the number of time periods T. We discuss an approach to analyze such data in Section 9.6. It is also common to assume that the factors, hence 
, are serially uncorrelated in factor analysis. In applications, if the observed returns are serially dependent, then the models in Chapter 8 can be used to remove the serial dependence.
In matrix form, the factor model in Eq. (9.1) can be written as
where 
is a row vector of loadings, and the joint model for the k assets at time t is
where 
, 
, 
is a k × m factor-loading matrix, and 
is the error vector with Cov(
, a k × k diagonal matrix. The covariance matrix of the return 
is then
The model presentation in Eq. (9.2) is in a cross-sectional regression form if the factors fjt are observed.
Treating the factor model in Eq. (9.1) as a time series, we have
for the ith asset (i = 1, … ,k), where 
, 
is a T-dimensional vector of ones, 
is a T × m matrix whose tth row is 
, and 
. The covariance matrix of 
is Cov(
, a T × T diagonal matrix.
Finally, we can rewrite Eq. (9.2) as
where 
and 
, which is a k × (m + 1) matrix. Taking the transpose of the prior equation and stacking all data together, we have
where 
is a T × k matrix of returns whose tth row is 
or, equivalently, whose ith column is 
of Eq. (9.3), 
is a T × (m + 1) matrix whose tth row is 
, and 
is a T × k matrix of specific factors whose tth row is 
. If the common factors 
are observed, then Eq. (9.4) is a special form of the multivariate linear regression (MLR) model; see Johnson and Wichern (2007). For a general MLR model, the covariance matrix of 
need not be diagonal.