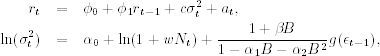3.8 The Exponential GARCH Model

To overcome some weaknesses of the GARCH model in handling financial time series, Nelson (1991) proposes the exponential GARCH (EGARCH) model. In particular, to allow for asymmetric effects between positive and negative asset returns, he considered the weighted innovation

(3.24)

where θ and γ are real constants. Both ϵt and |ϵt| − E(|ϵt|) are zero-mean iid sequences with continuous distributions. Therefore, E[g(ϵt)] = 0. The asymmetry of g(ϵt) can easily be seen by rewriting it as

where α0 is a constant, B is the back-shift (or lag) operator such that Bg(ϵt) = g(ϵt−1), and 1 + β1B + ⋯ + βs−1Bs−1 and 1 − α1B − ⋯ − αmBm are polynomials with zeros outside the unit circle and have no common factors. By outside the unit circle we mean that absolute values of the zeros are greater than 1. Again, Eq. (3.25) uses the usual ARMA parameterization to describe the evolution of the conditional variance of at. Based on this representation, some properties of the EGARCH model can be obtained in a similar manner as those of the GARCH model. For instance, the unconditional mean of is α0. However, the model differs from the GARCH model in several ways. First, it uses logged conditional variance to relax the positiveness constraint of model coefficients. Second, the use of g(ϵt) enables the model to respond asymmetrically to positive and negative lagged values of at. Some additional properties of the EGARCH model can be found in Nelson (1991).

To better understand the EGARCH model, let us consider the simple model with order (1,1):

(3.26)

where the ϵt are iid standard normal and the subscript of α1 is omitted. In this case, E(|ϵt|) = and the model for becomes

(3.27)

where . This is a nonlinear function similar to that of the threshold autoregressive (TAR) model of Tong (1978, 1990). It suffices to say that for this simple EGARCH model the conditional variance evolves in a nonlinear manner depending on the sign of at−1. Specifically, we have

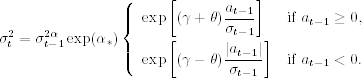
The coefficients (γ + θ) and (γ − θ) show the asymmetry in response to positive and negative at−1. The model is, therefore, nonlinear if θ ≠ 0. Since negative shocks tend to have larger impacts, we expect θ to be negative. For higher order EGARCH models, the nonlinearity becomes much more complicated. Cao and Tsay (1992) use nonlinear models, including EGARCH models, to obtain multistep-ahead volatility forecasts. We discuss nonlinearity in financial time series in Chapter 4.

3.8.1 Alternative Model Form

An alternative form for the EGARCH(m, s) model is

(3.28)

Here a positive at−i contributes αi(1 + γi)|ϵt−i| to the log volatility, whereas a negative at−i gives αi(1 − γi)|ϵt−i|, where ϵt−i = at−i/σt−i. The γi parameter thus signifies the leverage effect of at−i. Again, we expect γi to be negative in real applications. This is the model form used in S-Plus.

3.8.2 Illustrative Example

Nelson (1991) applies an EGARCH model to the daily excess returns of the value-weighted market index from the Center for Research in Security Prices from July 1962 to December 1987. The excess returns are obtained by removing monthly Treasury bill returns from the value-weighted index returns, assuming that the Treasury bill return was constant for each calendar day within a given month. There are 6408 observations. Denote the excess return by rt. The model used is as follows:

(3.29)

where is the conditional variance of at given Ft−1, Nt is the number of nontrading days between trading days t − 1 and t, α0 and w are real parameters, g(ϵt) is defined in Eq. (3.24), and ϵt follows a generalized error distribution in Eq. (3.10). Similar to a GARCH-M model, the parameter c in Eq. (3.29) is the risk premium parameter. Table 3.3 gives the parameter estimates and their standard errors of the model. The mean equation of model (3.29) has two features that are of interest. First, it uses an AR(1) model to take care of possible serial correlation in the excess returns. Second, it uses the volatility as a regressor to account for risk premium. The estimated risk premium is negative, but statistically insignificant.

Table 3.3 Estimated AR(1)–EGARCH(2,2) Model for Daily Excess Returns of Value-Weighted CRSP Market Index: July 1962–December 1987

3.8.3 Second Example

As another illustration, we consider the monthly log returns of IBM stock from January 1926 to December 1997 for 864 observations. An AR(1)–EGARCH(1,1) model is entertained and the fitted model is

(3.30)

(3.31)

where {ϵt} is a sequence of independent standard Gaussian random variates. All parameter estimates are statistically significant at the 5% level. For model checking, the Ljung–Box statistics give Q(10) = 6.31(0.71) and Q(20) = 21.4(0.32) for the standardized residual process ãt = at/σt and Q(10) = 4.13(0.90) and Q(20) = 15.93(0.66) for the squared process , where again the number in parentheses denotes p value. Therefore, there is no serial correlation or conditional heteroscedasticity in the standardized residuals of the fitted model. The prior AR(1)–EGARCH(1,1) model is adequate.

From the estimated volatility equation in (3.31) and using 0.7979, we obtain the volatility equation as

Taking antilog transformation, we have

This equation highlights the asymmetric responses in volatility to the past positive and negative shocks under an EGARCH model. For example, for a standardized shock with magnitude 2 (i.e., two standard deviations), we have

Therefore, the impact of a negative shock of size 2 standard deviations is about 37.4% higher than that of a positive shock of the same size. This example clearly demonstrates the asymmetric feature of EGARCH models. In general, the bigger the shock, the larger the difference in volatility impact.

Finally, we extend the sample period to include the log returns from 1998 to 2003 so that there are 936 observations and use S-Plus to fit an EGARCH(1,1) model. The results are given below.

S-Plus Demonstration

The following output has been edited:

The fitted GARCH(1,1) model is

(3.32)

where ϵt follows a GED distribution with parameter 1.5. This model is adequate and based on the Ljung–Box statistics of the standardized residual series and its squared process. As expected, the output shows that the estimated leverage effect is negative and is statistically significant at the 5% level with a t ratio of − 2.094.

3.8.4 Forecasting Using an EGARCH Model

We use the EGARCH(1,1) model to illustrate multistep-ahead forecasts of EGARCH models, assuming that the model parameters are known and the innovations are standard Gaussian. For such a model, we have

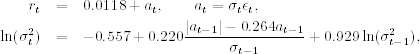
Taking exponentials, the model becomes

(3.33)

Let h be the forecast origin. For the 1-step-ahead forecast, we have

where all of the quantities on the right-hand side are known. Thus, the 1-step-ahead volatility forecast at the forecast origin h is simply = given earlier. For the 2-step-ahead forecast, Eq. (3.33) gives

Taking conditional expectation at time h, we have

where Eh denotes a conditional expectation taken at the time origin h. The prior expectation can be obtained as follows:

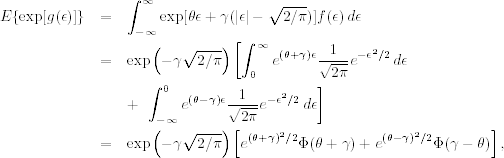
where f(ϵ) and Φ(x) are the probability density function and CDF of the standard normal distribution, respectively. Consequently, the 2-step-ahead volatility forecast is

Repeating the previous procedure, we obtain a recursive formula for a j-step-ahead forecast:

where . The values of Φ(θ + γ) and Φ(γ − θ) can be obtained from most statistical packages. Alternatively, accurate approximations to these values can be obtained by using the method in Appendix B of Chapter 6.

For illustration, consider the AR(1)–EGARCH(1,1) model of the previous section for the monthly log returns of IBM stock, ending December 1997. Using the fitted EGARCH(1,1) model, we can compute the volatility forecasts for the series. At the forecast origin t = 864, the forecasts are , = 5.82 × 10−3, = 5.63 × 10−3, and = 4.94 × 10−3. These forecasts converge gradually to the sample variance 4.37 × 10−3 of the shock process at of Eq. (3.30).