The first model that provides a systematic framework for volatility modeling is the ARCH model of Engle (1982). The basic idea of ARCH models is that (a) the shock at of an asset return is serially uncorrelated, but dependent, and (b) the dependence of at can be described by a simple quadratic function of its lagged values. Specifically, an ARCH(m) model assumes that
where {ϵt} is a sequence of independent and identically distributed (iid) random variables with mean zero and variance 1, α0 > 0, and αi ≥ 0 for i > 0. The coefficients αi must satisfy some regularity conditions to ensure that the unconditional variance of at is finite. In practice, ϵt is often assumed to follow the standard normal or a standardized Student-t or a generalized error distribution.
From the structure of the model, it is seen that large past squared shocks 
imply a large conditional variance 
for the innovation at. Consequently, at tends to assume a large value (in modulus). This means that, under the ARCH framework, large shocks tend to be followed by another large shock. Here I use the word tend because a large variance does not necessarily produce a large realization. It only says that the probability of obtaining a large variate is greater than that of a smaller variance. This feature is similar to the volatility clusterings observed in asset returns.
The ARCH effect also occurs in other financial time series. Figure 3.3 shows the time plots of (a) the percentage changes in Deutsche mark/U.S. dollar exchange rate measured in 10-minute intervals from June 5, 1989, to June 19, 1989, for 2488 observations, and (b) the squared series of the percentage changes. Big percentage changes occurred occasionally, but there were certain stable periods. Figure 3.4(a) shows the sample ACF of the percentage change series. Clearly, the series has no serial correlation. Figure 3.4(b) shows the sample PACF of the squared series of percentage change. It is seen that there are some big spikes in the PACF. Such spikes suggest that the percentage changes are not serially independent and have some ARCH effects.
Figure 3.3 (a) Time plot of 10-minute returns of exchange rate between Deutsche mark and U.S. dollar from June 5, 1989, to June 19, 1989, and (b) the squared returns.
Figure 3.4 (a) Sample autocorrelation function of return series of mark/dollar exchange rate and (b) sample partial autocorrelation function of squared returns.
Remark
Some authors use ht to denote the conditional variance in Eq. (3.5). In this case, the shock becomes 
.
3.4.1 Properties of ARCH Models
To understand the ARCH models, it pays to carefully study the ARCH(1) model
where α0 > 0 and α1 ≥ 0. First, the unconditional mean of at remains zero because
Second, the unconditional variance of at can be obtained as
Because at is a stationary process with E(at) = 0, Var(at) = Var(at−1) = 
. Therefore, we have Var(at) = α0 + α1Var(at) and Var(at) = α0/(1 − α1). Since the variance of at must be positive, we require 0 ≤ α1 < 1. Third, in some applications, we need higher order moments of at to exist and, hence, α1 must also satisfy some additional constraints. For instance, to study its tail behavior, we require that the fourth moment of at is finite. Under the normality assumption of ϵt in Eq. (3.5), we have
Therefore,
If at is fourth-order stationary with 
, then we have
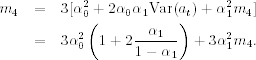
Consequently,
This result has two important implications: (a) since the fourth moment of at is positive, we see that α1 must also satisfy the condition 
; that is, 
; and (b) the unconditional kurtosis of at is
Thus, the excess kurtosis of at is positive and the tail distribution of at is heavier than that of a normal distribution. In other words, the shock at of a conditional Gaussian ARCH(1) model is more likely than a Gaussian white noise series to produce “outliers.” This is in agreement with the empirical finding that “outliers” appear more often in asset returns than that implied by an iid sequence of normal random variates.
These properties continue to hold for general ARCH models, but the formulas become more complicated for higher order ARCH models. The condition αi ≥ 0 in Eq. (3.5) can be relaxed. It is a condition to ensure that the conditional variance 
is positive for all t. In fact, a natural way to achieve positiveness of the conditional variance is to rewrite an ARCH(m) model as
where Am, t−1 = (at−1, … , at−m)′ and Ω is an m × m nonnegative definite matrix. The ARCH(m) model in Eq. (3.5) requires Ω to be diagonal. Thus, Engle's model uses a parsimonious approach to approximate a quadratic function. A simple way to achieve Eq. (3.6) is to employ a random-coefficient model for at; see the CHARMA and RCA models discussed later.
3.4.2 Weaknesses of ARCH Models
The advantages of ARCH models include properties discussed in the previous section. The model also has some weaknesses:
1. The model assumes that positive and negative shocks have the same effects on volatility because it depends on the square of the previous shocks. In practice, it is well known that the price of a financial asset responds differently to positive and negative shocks.
2. The ARCH model is rather restrictive. For instance, 
of an ARCH(1) model must be in the interval [0, 
] if the series has a finite fourth moment. The constraint becomes complicated for higher order ARCH models. In practice, it limits the ability of ARCH models with Gaussian innovations to capture excess kurtosis.
3. The ARCH model does not provide any new insight for understanding the source of variations of a financial time series. It merely provides a mechanical way to describe the behavior of the conditional variance. It gives no indication about what causes such behavior to occur.
4. ARCH models are likely to overpredict the volatility because they respond slowly to large isolated shocks to the return series.
3.4.3 Building an ARCH Model
Among volatility models, specifying an ARCH model is relatively easy. Details are given below.
Order Determination
If an ARCH effect is found to be significant, one can use the PACF of 
to determine the ARCH order. Using PACF of 
to select the ARCH order can be justified as follows. From the model in Eq. (3.5), we have
For a given sample, 
is an unbiased estimate of 
. Therefore, we expect that 
is linearly related to 
in a manner similar to that of an autoregressive model of order m. Note that a single 
is generally not an efficient estimate of 
, but it can serve as an approximation that could be informative in specifying the order m.
Alternatively, define 
. It can be shown that {ηt} is an uncorrelated series with mean 0. The ARCH model then becomes
which is in the form of an AR(m) model for 
, except that {ηt} is not an iid series. From Chapter 2, PACF of 
is a useful tool to determine the order m. Because {ηt} are not identically distributed, the least-squares estimates of the prior model are consistent but not efficient. The PACF of 
may not be effective when the sample size is small.
Estimation
Several likelihood functions are commonly used in ARCH estimation, depending on the distributional assumption of ϵt. Under the normality assumption, the likelihood function of an ARCH(m) model is
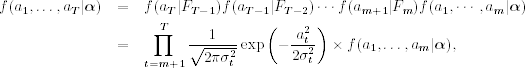
where α = (α0, α1, … , αm)′ and f(a1, … , am|α) is the joint probability density function of a1, … , am. Since the exact form of f(a1, … , am|α) is complicated, it is commonly dropped from the prior likelihood function, especially when the sample size is sufficiently large. This results in using the conditional-likelihood function
where 
can be evaluated recursively. We refer to estimates obtained by maximizing the prior likelihood function as the conditional maximum-likelihood estimates (MLEs) under normality.
Maximizing the conditional-likelihood function is equivalent to maximizing its logarithm, which is easier to handle. The conditional log-likelihood function is
Since the first term ln(2π) does not involve any parameters, the log-likelihood function becomes
where 
can be evaluated recursively.
In some applications, it is more appropriate to assume that ϵt follows a heavy-tailed distribution such as a standardized Student-t distribution. Let xv be a Student-t distribution with v degrees of freedom. Then Var(xv) = v/(v − 2) for v > 2, and we use 
. The probability density function of ϵt is
where Γ(x) is the usual gamma function (i.e., 
). Using at = σtϵt, we obtain the conditional-likelihood function of at as
where v > 2 and Am = (a1, a2, … , am). We refer to the estimates that maximize the prior likelihood function as the conditional MLEs under t distribution. The degrees of freedom of the t distribution can be specified a priori or estimated jointly with other parameters. A value between 4 and 8 is often used if it is prespecified.
If the degrees of freedom v of the Student-t distribution is prespecified, then the conditional log-likelihood function is
If one wishes to estimate v jointly with other parameters, then the log-likelihood function becomes
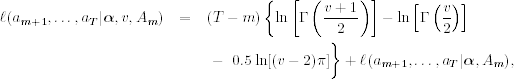
where the second term is given in Eq. (3.8).
Besides fat tails, empirical distributions of asset returns may also be skewed. To handle this additional characteristic of asset returns, the Student-t distribution has been modified to become a skew-Student-t distribution. There are multiple versions of skew-Student-t distribution, but we shall adopt the approach of Fernández and Steel (1998), which can introduce skewness into any continuous unimodal and symmetric (with respect to 0) univariate distribution. Specifically, for the innovation ϵt of an ARCH process, Lambert and Laurent (2001) apply the Fernández and Steel method to the standardized Student-t distribution in Eq. (3.7) to obtain a standardized skew-Student-t distribution. The resulting probability density function is
where f(·) is the probability density function (pdf) of the standardized Student-t distribution in Eq. (3.7), ξ is the skewness parameter, v > 2 is the degrees of freedom, and the parameters ϱ and 
are given below:
In Eq. (3.9), ξ2 is equal to the ratio of probability masses above and below the mode of the distribution and, hence, it is a measure of the skewness.
Finally, ϵt may assume a generalized error distribution (GED) with probability density function
where Γ(·) is the gamma function and λ = [2(−2/v)Γ(1/v)/Γ(3/v)]1/2. This distribution reduces to a Gaussian distribution if v = 2, and it has heavy tails when v < 2. The conditional log-likelihood function ℓ(am+1, … , aT|α, Am) can easily be obtained.
Remark
Skew Student-t, skew normal, and skew GED distributions are available in the fGarch package of Rmetrics. The commands are sstd, snorm, and sged, respectively. See the R demonstration below for an example.
Model Checking
For a properly specified ARCH model, the standardized residuals
form a sequence of iid random variables. Therefore, one can check the adequacy of a fitted ARCH model by examining the series {ãt}. In particular, the Ljung–Box statistics of ãt can be used to check the adequacy of the mean equation and that of 
can be used to test the validity of the volatility equation. The skewness, kurtosis, and quantile-to-quantile plot (i.e., QQ plot) of {ãt} can be used to check the validity of the distribution assumption. Many residual plots are available in S-Plus for model checking.
Forecasting
Forecasts of the ARCH model in Eq. (3.5) can be obtained recursively as those of an AR model. Consider an ARCH(m) model. At the forecast origin h, the 1-step-ahead forecast of 
is
The 2-step-ahead forecast is
and the ℓ-step-ahead forecast for 
is
(3.11) 
where 
if ℓ − i ≤ 0.
3.4.4 Some Examples
In this section, we illustrate ARCH modeling by considering two examples.
Example 3.1
We first apply the modeling procedure to build a simple ARCH model for the monthly log returns of Intel stock. The sample ACF and PACF of the squared returns in Figure 3.2 clearly show the existence of conditional heteroscedasticity. This is confirmed by the ARCH test shown in Section 3.3.1, and we proceed to identify the order of an ARCH model. The sample PACF in Figure 3.2(d) indicates that an ARCH(3) model might be appropriate. Consequently, we specify the model
for the monthly log returns of Intel stock. Assuming that ϵt are iid standard normal, we obtain the fitted model
where the standard errors of the parameters are 0.0057, 0.0010, 0.0757, 0.0480, and 0.0688, respectively; see the output below. While the estimates meet the general requirement of an ARCH(3) model, the estimates of α2 and α3 appear to be statistically nonsignificant at the 5% level. Therefore, the model can be simplified.
S-Plus Demonstration
The following output has been edited and % marks explanation:
> module(finmetrics)
> da=read.table(“m-intc7308.txt”,header=T)
> intc=log(da[,2]+1)
> arch3.fit=garch(intc∼1,∼garch(3,0))
> summary(arch3.fit)
garch(formula.mean = intc ∼ 1, formula.var = ∼ garch(3, 0))
Mean Equation: structure(.Data = intc ∼ 1, class = “formula”)
Conditional Variance Equation:structure(.Data=∼garch(3,0),..)
Conditional Distribution: gaussian
--------------------------------------------------------------
Estimated Coefficients:
--------------------------------------------------------------
Value Std.Error t value Pr(>|t|)
C 0.01216 0.0056986 2.1341 0.033402
A 0.01058 0.0009643 10.9739 0.000000
ARCH(1) 0.21307 0.0756708 2.8157 0.005093
ARCH(2) 0.07698 0.0480170 1.6032 0.109638
ARCH(3) 0.05988 0.0688081 0.8703 0.384628
--------------------------------------------------------------
> arch1=garch(intc∼1,∼garch(1,0))
> summary(arch1)
garch(formula.mean = intc ∼ 1, formula.var = ∼ garch(1, 0))
Conditional Distribution: gaussian
--------------------------------------------------------------
Estimated Coefficients:
--------------------------------------------------------------
Value Std.Error t value Pr(>|t|)
C 0.01261 0.0052624 2.397 1.695e-02
A 0.01113 0.0009971 11.164 0.000e+00
ARCH(1) 0.35602 0.0761267 4.677 3.912e-06
--------------------------------------------------------------
AIC(3) = -570.0179, BIC(3) = -557.8126
Ljung-Box test for standardized residuals:
--------------------------------------------------------------
Statistic P-value Chiˆ2-d.f.
14.26 0.2844 12
Ljung-Box test for squared standardized residuals:
--------------------------------------------------------------
Statistic P-value Chiˆ2-d.f.
32.11 0.001329 12
> stres=arch1$residuals/arch1$sigma.t %standardized residuals
> autocorTest(stres,lag=10)
Test for Autocorrelation: Ljung-Box
Null Hypothesis: no autocorrelation
Test Statistics:
Test Stat 12.6386, p.value 0.2446
Dist. under Null: chi-square with 10 degrees of freedom
> archTest(stres,lag=10)
Test for ARCH Effects: LM Test
Null Hypothesis: no ARCH effects
Test Statistics:
Test Stat 14.7481, p.value 0.1415
Dist. under Null: chi-square with 10 degrees of freedom
> arch1$asymp.sd %Obtain unconditional standard error
[1] 0.1314698
> plot(arch1) % Obtain various plots, including the
% fitted volatility series.
Dropping the two nonsignificant parameters, we obtain the model
where the standard errors of the parameters are 0.0053, 0.0010, and 0.0761, respectively. All the estimates are highly significant. Figure 3.5 shows the standardized residuals {ãt} and the sample ACF of some functions of {ãt}. The Ljung–Box statistics of standardized residuals give Q(10) = 12.64 with a p value of 0.24 and those of 
give Q(10) = 14.75 with a p value of 0.14. See the output. Consequently, the ARCH(1) model in Eq. (3.12) is adequate for describing the conditional heteroscedasticity of the data at the 5% significance level.
Figure 3.5 Model checking statistics of Gaussian ARCH(1) model in Eq. (3.12) for monthly log returns of Intel stock from January 1973 to December 2008: Parts (a), (b), and (c) show sample ACF of standardized residuals, their squared series, and absolute series, respectively; part (d) is time plot of standardized residuals.
The ARCH(1) model in Eq. (3.12) has some interesting properties. First, the expected monthly log return for Intel stock is about 1.26%, which is remarkable, especially since the data span includes the period after the Internet bubble. Second, 
= 
so that the unconditional fourth moment of the monthly log return of Intel stock exists. Third, the unconditional standard deviation of rt is 
Finally, the ARCH(1) model can be used to predict the monthly volatility of Intel stock returns.
t Innovation
For comparison, we also fit an ARCH(1) model with Student-t innovations to the series. The resulting model is
where the standard errors of the parameters are 0.0053, 0.0017, and 0.1120, respectively. The estimated degrees of freedom is 6.01 with standard error 1.50. All the estimates are significant at the 5% level. The unconditional standard deviation of at is 
, which is close to that obtained under normality. The Ljung–Box statistics of the standardized residuals give Q(12) = 14.88 with a p value of 0.25, confirming that the mean equation is adequate. However, the Ljung–Box statistics for the squared standardized residuals show Q(12) = 35.42 with a p value of 0.0004. The volatility equation is inadequate at the 1% level. Further analysis shows that Q(10) = 15.90 with a p value of 0.10 for the squared standardized residuals. The inadequancy of the volatility equation is due to a large lag-12 ACF (ρ12 = 0.188) of the squared standardized residuals.
Comparing models (3.12) and (3.13), we see that (a) using a heavy-tailed distribution for ϵt reduces the ARCH coefficient, and (b) the difference between the two models is small for this particular instance. Finally, a more appropriate conditional heteroscedastic model for the monthly log returns of Intel stock is a GARCH(1,1) model, which is discussed in the next section.
S-Plus Demonstration
Note the following output with t innovations:
> arch1t=garch(intc∼1,∼garch(1,0),cond.dist=“t”)
> summary(arch1t)
Call:
garch(formula.mean=intc∼1,formula.var=∼garch(1,0),
cond.dist=“t”)
Mean Equation: structure(.Data = intc ∼ 1, class = “formula”)
Cond. Variance Equation:structure(.Data=∼ garch(1,0), ...)
Cond. Distribution: t
with estimated parameter 6.012769 and standard error 1.502179
--------------------------------------------------------------
Estimated Coefficients:
--------------------------------------------------------------
Value Std.Error t value Pr(>|t|)
C 0.01688 0.005288 3.193 1.512e-03
A 0.01195 0.001667 7.169 3.345e-12
ARCH(1) 0.28445 0.111998 2.540 1.145e-02
--------------------------------------------------------------
AIC(4) = -597.3379, BIC(4) = -581.0642
Ljung-Box test for standardized residuals:
--------------------------------------------------------------
Statistic P-value Chiˆ2-d.f.
14.88 0.2482 12
Ljung-Box test for squared standardized residuals:
--------------------------------------------------------------
Statistic P-value Chiˆ2-d.f.
35.42 0.0004014 12
In S-Plus, the command garch allows for several conditional distributions. They are specified by cond.dist = “t” or “ged”. The default is Gaussian. The R output is given below. The estimates are close to those of S-Plus.
R Demonstration
The following output uses the fGarch package with command garchFit and % denotes explanation:
> da=read.table(“m-intc7308.txt”,header=T)
> library(fGarch) % Load the package
> intc=log(da[,2]+1)
> m1=garchFit(intc∼garch(1,0),data=intc,trace=F)
> summary(m1) % Obtain results
Title:
GARCH Modelling
Call:
garchFit(formula=intc∼garch(1,0), data=intc, trace=F)
Mean and Variance Equation: data ∼ garch(1, 0) [data = intc]
Conditional Distribution: norm
Coefficient(s):
mu omega alpha1
0.012637 0.011195 0.379492
Std. Errors:
based on Hessian
Error Analysis:
Estimate Std. Error t value Pr(>|t|)
mu 0.012637 0.005428 2.328 0.01990 *
omega 0.011195 0.001239 9.034 < 2e-16 ***
alpha1 0.379492 0.115534 3.285 0.00102 **
---
Log Likelihood:
288.0589 normalized: 0.6668031
Standardised Residuals Tests: %Model checking
Statistic p-Value
Jarque-Bera Test R Chiˆ2 137.919 0
Shapiro-Wilk Test R W 0.9679255 4.025172e-08
Ljung-Box Test R Q(10) 12.54002 0.2505382
Ljung-Box Test R Q(15) 21.33508 0.1264607
Ljung-Box Test R Q(20) 23.19679 0.2792354
Ljung-Box Test Rˆ2 Q(10) 16.0159 0.09917815
Ljung-Box Test Rˆ2 Q(15) 36.08022 0.001721296
Ljung-Box Test Rˆ2 Q(20) 37.43683 0.01036728
LM Arch Test R TRˆ2 26.57744 0.008884587
Information Criterion Statistics:
AIC BIC SIC HQIC
-1.319717 -1.291464 -1.319813 -1.308563
> predict(m1,5) % Obtain 1 to 5-step predictions
meanForecast meanError standardDeviation
1 0.01263656 0.1278609 0.1098306
2 0.01263656 0.1278609 0.1255897
3 0.01263656 0.1278609 0.1310751
4 0.01263656 0.1278609 0.1330976
5 0.01263656 0.1278609 0.1338571
% The next command fits a GARCH(1,1) model
> m2=garchFit(intc∼garch(1,1),data=intc,trace=F)
> summary(m2) % output edited.
Coefficient(s):
mu omega alpha1 beta1
0.01073352 0.00095445 0.08741989 0.85118414
Error Analysis:
Estimate Std. Error t value Pr(>|t|)
mu 0.0107335 0.0055289 1.941 0.05222 .
omega 0.0009544 0.0003989 2.392 0.01674 *
alpha1 0.0874199 0.0269810 3.240 0.00120 **
beta1 0.8511841 0.0393702 21.620 < 2e-16 ***
---
Standardised Residuals Tests:
Statistic p-Value
Jarque-Bera Test R Chiˆ2 165.5740 0
Shapiro-Wilk Test R W 0.9712087 1.626824e-07
Ljung-Box Test R Q(10) 8.267633 0.6027128
Ljung-Box Test R Q(15) 14.42612 0.4934871
Ljung-Box Test R Q(20) 15.13331 0.7687297
Ljung-Box Test Rˆ2 Q(10) 0.9891848 0.9998363
Ljung-Box Test Rˆ2 Q(15) 11.36596 0.7262473
Ljung-Box Test Rˆ2 Q(20) 12.68143 0.8906302
LM Arch Test R TRˆ2 10.70199 0.5546164
% The next command fits an ARCH(1) model with Student-t dist.
> m3=garchFit(intc∼garch(1,0),data=intc,trace=F,
cond.dist=‘std’)
> summary(m3) % Output shortened.
Call:
garchFit(formula=intc∼garch(1,0), data=intc, cond.dist=“std”,
trace = F)
Mean and Variance Equation: data ∼ garch(1, 0) [data = intc]
Conditional Distribution: std % Student-t distribution
Coefficient(s):
mu omega alpha1 shape
0.016731 0.011939 0.285320 6.015195
Error Analysis:
Estimate Std. Error t value Pr(>|t|)
mu 0.016731 0.005302 3.155 0.001603 **
omega 0.011939 0.001603 7.449 9.4e-14 ***
alpha1 0.285320 0.110607 2.580 0.009892 **
shape 6.015195 1.562620 3.849 0.000118 ***
% Degrees of freedom
% The next command fits an ARCH(1) model with skew
%Student-t dist.
> m4=garchFit(intc∼garch(1,0),data=intc,cond.dist=‘sstd’,
trace=F)
% Next, fit an ARMA(1,0)+GARCH(1,1) model with
% Gaussian noises.
> m5=garchFit(intc∼arma(1,0)+garch(1,1),data=intc,trace=F)
R Demonstration
The following output was generated with Ox and [email protected] package and % denotes explanation:
> source(“garchoxfitR.txt”)
% In G@RCH package, an ARCH(1) model is specified as
% GARCH(0,1).
> m1=garchOxFit(formula.mean=∼arma(0,0),
formula.var=∼garch(0,1), series=intc)
% ** SPECIFICATIONS **
Dependent variable : X
Mean Equation : ARMA (0, 0) model.
No regressor in the mean
Variance Equation : GARCH (0, 1) model.
No regressor in the variance
The distribution is a Gauss distribution.
Maximum Likelihood Estimation(Std.Errors based on 2nd deriv.)
Coefficient Std.Error t-value t-prob
Cst(M) 0.012630 0.0054130 2.333 0.0201
Cst(V) 0.011129 0.0012355 9.007 0.0000
ARCH(Alpha1) 0.387223 0.11688 3.313 0.0010
% ** TESTS **
Q-Statistics on Standardized Residuals
Q(10)=12.4952 [0.2532785], Q(20)=23.1210 [0.2828934]
H0: No serial correlation ==> Accept H0 when prob. is High.
------------
Q-Statistics on Squared Standardized Residuals
--> P-values adjusted by 1 degree(s) of freedom
Q(10)=15.7849 [0.0715122], Q( 20)=37.0238 [0.0078807]
------------
ARCH 1-10 test: F(10,410)= 1.4423 [0.1592]
------------
% Apply Student-t distribution
> m2=garchOxFit(formula.mean=∼arma(0,0),
formula.var=∼garch(0,1),
series=intc,cond.dist=“t”)
% ** SPECIFICATIONS **
Dependent variable : X
Mean Equation : ARMA (0, 0) model.
No regressor in the mean
Variance Equation : GARCH (0, 1) model.
No regressor in the variance
The distribution is a Student distribution, with 6.02272 df.
Maximum Likelihood Estimation(Std.Errors based on 2nd deriv.)
Coefficient Std.Error t-value t-prob
Cst(M) 0.016702 0.0052934 3.155 0.0017
Cst(V) 0.011870 0.0015969 7.433 0.0000
ARCH(Alpha1) 0.292318 0.11223 2.605 0.0095
Student(DF) 6.022723 1.5663 3.845 0.0001
** TESTS **
Q-Statistics on Standardized Residuals
Q(10)=13.0837 [0.2190281], Q(20)=24.0724 [0.2392436]
------------
Q-Statistics on Squared Standardized Residuals
--> P-values adjusted by 1 degree(s) of freedom
Q(10)=18.6982 [0.0278845], Q( 20)=41.7182 [0.0019343]
Example 3.2
Consider the percentage changes of the exchange rate between mark and dollar in 10-minute intervals. The data are shown in Figure 3.3(a). As shown in Figure 3.4(a), the series has no serial correlations. However, the sample PACF of the squared series 
shows some big spikes, especially at lags 1 and 3. There are some large PACF at higher lags, but the lower order lags tend to be more important. Following the procedure discussed in the previous section, we specify an ARCH(3) model for the series. Using the conditional Gaussian likelihood function, we obtain the fitted model rt = 0.0018 + σtϵt and
where all the estimates in the volatility equation are statistically significant at the 5% significant level, and the standard errors of the parameters are 0.47 × 10−6, 0.017, 0.016, and 0.014, respectively. Model checking, using the standardized residual ãt, indicates that the model is adequate.