Appendix B: R and S-Plus Commands for Neural Network
The following commands are used in R or S-Plus to build the 3–2–1 skip-layer feed-forward network of Example 4.7. A line starting with # denotes a comment. The data file is m-ibmln.txt. The library used is nnet.
# load the data into R or S-Plus workspace.
x_scan(file=‘m-ibmln.txt’)
# select the output: r(t)
y_x[4:864]
# obtain the input variables: r(t-1), r(t-2), and r(t-3)
ibm.x_cbind(x[3:863]_,x[2:862],x[1:861])
# build a 3-2-1 network with skip layer connections
# and linear output.
ibm.nn_nnet(ibm.x,y,size=2,linout=T,skip=T,maxit=10000,
decay=1e-2,reltol=1e-7,abstol=1e-7,range=1.0)
# print the summary results of the network
summary(ibm.nn)
# compute & print the residual sum of squares.
sse_sum((y-predict(ibm.nn,ibm.x))ˆ2)
print(sse)
#eigen(nnet.Hess(ibm.nn,ibm.x,y),T)$values
# setup the input variables in the forecasting subsample
ibm.p_cbind(x[864:887],x[863:886],x[862:885])
# compute the forecasts
yh_predict(ibm.nn,ibm.p)
# The observed returns in the forecasting subsample
yo_x[865:888]
# compute & print the sum of squares of forecast errors
ssfe_sum((yo-yh)ˆ2)
print(ssfe)
# quit S-Plus or R
q()
Exercises
4.1 Consider the daily simple returns of Johnson & Johnson stock from January 1998 to December 2008. The data are in the file d-jnj9808.txt or can be obtained from CRSP. Convert the returns into log returns in percentage. (a) Build a GJR model for the log return series. Write down the fitted model. Is the leverage effect significant at the 1% level? (b) Build a general threshold volatility model for the log return series. (c) Compare the two TGARCH models.
4.2 Consider the monthly simple returns of General Electric (GE) stock from January 1926 to December 2008 with 996 observations. You may download the data from CRSP or use the file m-ge2608.txt on the Web. Convert the returns into log returns in percentages. Build a TGARCH model with GED innovations for the series using at−1 as the threshold variable with zero threshold, where at−1 is the shock at time t − 1. Write down the fitted model. Is the leverage effect significant at the 5% level?
4.3 Suppose that the monthly log returns of GE stock, measured in percentages, follow a smooth threshold IGARCH(1,1) model. For the sampling period from January 1926 to December 2008, the fitted model is
where all of the estimates are highly significant, the coefficient 10 in the exponent is fixed a priori to simplify the estimation, and {ϵt} are iid N(0, 1). Assume that a996 = − 5.06 and 
= 50.5. What is the 1-step-ahead volatility forecast 
? Suppose instead that a996 = 5.06. What is the 1-step-ahead volatility forecast 
?
4.4 Suppose that the monthly log returns, in percentages, of a stock follow the following Markov switching model:
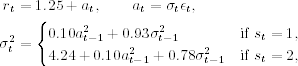
where the transition probabilities are
Suppose that a100 = 6.0, 
= 50.0, and s100 = 2 with probability 1.0. What is the 1-step-ahead volatility forecast at the forecast origin t = 100? Also, if the probability of s100 = 2 is reduced to 0.8, what is the 1-step-ahead volatility forecast at the forecast origin t = 100?
4.5 Consider the monthly simple returns of GE stock from January 1926 to December 2008. Use the last three years of data for forecasting evaluation.
a. Using lagged returns rt−1, rt−2, rt−3 as input, build a 3–2–1 feed-forward network to forecast 1-step-ahead returns. Calculate the mean squared error of forecasts.
b. Again, use lagged returns rt−1, rt−2, rt−3 and their signs (directions) to build a 6–5–1 feed-forward network to forecast the 1-step ahead direction of GE stock price movement with 1 denoting upward movement. Calculate the mean squared error of forecasts.
Note: Let rtn denote a time series in R or S-Plus. To create a direction variable for rtn, use the command
drtn = ifelse(rtn > 0, 1, 0)
4.6 Because of the existence of inverted yield curves in the term structure of interest rates, the spread of interest rates should be nonlinear. To verify this, consider the weekly U.S. interest rates of (a) Treasury 1-year constant maturity rate and (b) Treasury 3-year constant maturity rate. As in Chapter 2, denote the two interest rates by r1t and r3t, respectively, and the data span is from January 5, 1962, to April 10, 2009. The data are in files w-gs3yr.txt and w-gs1yr.txt on the Web and can be obtained from the Federal Reserve Bank of St. Louis.
a. Let st = r3t − r1t be the spread in log interest rates. Is {st} linear? Perform some nonlinearity tests and draw the conclusion using the 5% significance level.
b. Let 
be the change in interest rate spread. Is 
linear? Perform some nonlinearity tests and draw the conclusion using the 5% significance level.
c. Build a threshold model for the st series and check the fitted model.
d. Build a threshold model for the 
series and check the fitted model.
Akaike, H. (1974). A new look at the statistical model identification. IEEE Transactions on Automatic Control AC-19: 716–723.
Andrews, D. W. K. and Ploberger, W. (1994). Optimal tests when a nuisance parameter is present only under the alternative. Econometrica 62: 1383–1414.
Brock, W., Dechert, W. D., and Scheinkman, J. (1987). A test for independence based on the correlation dimension. Working paper, Department of Economics, University of Wisconsin, Madison.
Brock, W., Hsieh, D. A., and LeBaron, B. (1991). Nonlinear Dynamics, Chaos and Instability: Statistical Theory and Economic Evidence. MIT Press, Cambridge, MA.
Bryson, A. E. and Ho, Y. C. (1969). Applied Optimal Control. Blaisdell, New York
Cai, Z., Fan, J., and Yao, Q. (2000). Functional-coefficient regression models for nonlinear time series. Journal of the American Statistical Association 95: 941–956.
Carlin, B. P., Polson, N. G., and Stoffer, D. S. (1992). A Monte Carlo approach to nonnormal and nonlinear state space modeling. Journal of the American Statistical Association 87: 493–500.
Chan, K. S. (1991). Percentage points of likelihood ratio tests for threshold autoregression. Journal of the Royal Statistical Society Series B 53: 691–696.
Chan, K. S. (1993). Consistency and limiting distribution of the least squares estimator of a threshold autoregressive model. Annals of Statistics 21: 520–533.
Chan, K. S. and Tong, H. (1986). On estimating thresholds in autoregressive models. Journal of Time Series Analysis 7: 179–190.
Chan, K. S. and Tsay, R. S. (1998). Limiting properties of the conditional least squares estimator of a continuous TAR model. Biometrika 85: 413–426.
Chen, C., McCulloch, R. E., and Tsay, R. S. (1997). A unified approach to estimating and modeling univariate linear and nonlinear time series. Statistica Sinica 7: 451–472.
Chen, R. and Tsay, R. S. (1991). On the ergodicity of TAR(1) processes. Annals of Applied Probability 1: 613–634.
Chen, R. and Tsay, R. S. (1993a). Functional-coefficient autoregressive models. Journal of the American Statistical Association 88: 298–308.
Chen, R. and Tsay, R. S. (1993b). Nonlinear additive ARX models. Journal of the American Statistical Association 88: 955–967.
Chen, R., Liu, J., and Tsay, R. S. (1995). Additivity tests for nonlinear autoregressive models. Biometrika (1995) 82: 369–383.
Chen, T. and Chen, H. (1995). Universal approximation to nonlinear operators by neural networks with arbitrary activation functions and its application to dynamical systems. IEEE Transactions on Neural Networks 6: 911–917.
Cheng, B. and Titterington, D. M. (1994). Neural networks: A review from a statistical perspective. Statistical Science 9: 2–54.
Clements, M. P. and Hendry, D. F. (1993). On the limitations of comparing mean square forecast errors. Journal of Forecasting 12: 617–637.
Cleveland, W. S. (1979). Robust locally weighted regression and smoothing scatterplots. Journal of the American Statistical Association 74: 829–836.
Dahl, C. M. and Hylleberg, S. (1999). Specifying nonlinear econometric models by flexible regression models and relative forecast performance. Working paper, Department of Economics, University of Aarhus, Denmark.
Davis, R. B. (1987). Hypothesis testing when a nuisance parameter is present only under the alternative. Biometrika 74: 33–43.
Engle, R. F. (1982). Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflations. Econometrica 50: 987–1007.
Epanechnikov, V. (1969). Nonparametric estimates of a multivariate probability density. Theory of Probability and Its Applications 14: 153–158.
Fan, J. (1993). Local linear regression smoother and their minimax efficiencies. Annals of Statistics 21: 196–216.
Fan, J. and Yao, Q. (2003). Nonlinear Time Series: Nonparametric and Parametric Methods. Springer, New York.
Gelfand, A. E. and Smith, A. F. M. (1990). Sampling-based approaches to calculating marginal densities. Journal of the American Statistical Association 85: 398–409.
Granger, C. W. J. and Andersen, A. P. (1978). An Introduction to Bilinear Time Series Models. Vandenhoek and Ruprecht, Gottingen.
Hamilton, J. D. (1989). A new approach to the economic analysis of nonstationary time series and the business cycle. Econometrica 57: 357–384.
Hamilton, J. D. (1990). Analysis of time series subject to changes in regime. Journal of Econometrics 45: 39–70.
Hamilton, J. D. (1994). Time Series Analysis. Princeton University Press, Princeton, NJ.
Hansen, B. E. (1997). Inference in TAR models. Studies in Nonlinear Dynamics and Econometrics 1: 119–131.
Härdle, W. (1990). Applied Nonparametric Regression. Cambridge University Press, New York.
Hinich, M. (1982). Testing for Gaussianity and linearity of a stationary time series. Journal of Time Series Analysis 3: 169–176.
Hornik, K. (1993). Some new results on neural network approximation. Neural Networks 6: 1069–1072.
Hornik, K., Stinchcombe, M., and White, H. (1989). Multilayer feedforward networks are universal approximators. Neural Networks 2: 359–366.
Hsieh, D. A. (1989). Testing for nonlinear dependence in daily foreign exchange rates. Journal of Business 62: 339–368.
Keenan, D. M. (1985). A Tukey non-additivity-type test for time series nonlinearity. Biometrika 72: 39–44.
Kitagawa, G. (1998). A self-organizing state space model. Journal of the American Statistical Association 93: 1203–1215.
Lewis, P. A. W. and Stevens, J. G. (1991). Nonlinear modeling of time series using multivariate adaptive regression spline (MARS). Journal of the American Statistical Association 86: 864–877.
Liu, J. and Brockwell, P. J. (1988). On the general bilinear time-series model. Journal of Applied Probability 25: 553–564.
Luukkonen, R., Saikkonen, P., and Teräsvirta (1988). Testing linearity against smooth transition autoregressive models. Biometrika 75: 491–499.
McCulloch, R. E. and Tsay, R. S. (1993). Bayesian inference and prediction for mean and variance shifts in autoregressive time series. Journal of the American Statistical Association 88: 968–978.
McCulloch, R. E. and Tsay, R. S. (1994). Statistical inference of macroeconomic time series via Markov switching models. Journal of Time Series Analysis 15: 523–539.
McLeod, A. I. and Li, W. K. (1983). Diagnostic checking ARMA time series models using squared-residual autocorrelations. Journal of Time Series Analysis 4: 269–273.
Montgomery, A. L., Zarnowitz, V., Tsay, R. S., and Tiao, G. C. (1998). Forecasting the U.S. unemployment rate, Journal of the American Statistical Association 93: 478–493.
Nadaraya, E. A. (1964). On estimating regression. Theory and Probability Application 10: 186–190.
Petruccelli, J. and Woolford, S. W. (1984). A threshold AR(1) model. Journal of Applied Probability 21: 270–286.
Potter, S. M. (1995). A nonlinear approach to U.S. GNP. Journal of Applied Econometrics 10: 109–125.
Priestley, M. B. (1980). State-dependent models: A general approach to nonlinear time series analysis. Journal of Time Series Analysis 1: 47–71.
Priestley, M. B. (1988). Non-linear and Non-stationary Time Series Analysis, Academic Press, London, UK.
Ramsey, J. B. (1969). Tests for specification errors in classical linear least squares regression analysis. Journal of the Royal Statistical Society Series B 31: 350–371.
Ripley, B. D. (1993). Statistical aspects of neural networks. In O. E. Barndorff-Nielsen, J. L. Jensen, and W. S. Kendall (eds.). Networks and Chaos—Statistical and Probabilistic Aspects, pp. 40–123. Chapman and Hall, London, UK.
SubbaRao, T. and Gabr, M. M. (1984). An Introduction to Bispectral Analysis and Bilinear Time Series Models, Lecture Notes in Statistics, vol. 24. Springer, New York.
Teräsvirta, T. (1994). Specification, estimation, and evaluation of smooth transition autoregressive models. Journal of the American Statistical Association 89: 208–218.
Tiao, G. C. and Tsay, R. S. (1994). Some advances in nonlinear and adaptive modeling in time series. Journal of Forecasting 13: 109–131.
Tong, H. (1978). On a threshold model. In C. H. Chen (ed.). Pattern Recognition and Signal Processing. Sijhoff & Noordhoff, Amsterdam.
Tong, H. (1983). Threshold Models in Nonlinear Time Series Analysis, Lecture Notes in Statistics, Springer, New York.
Tong, H. (1990). Non-Linear Time Series: A Dynamical System Approach, Oxford University Press, Oxford, UK.
Tsay, R. S. (1986). Nonlinearity tests for time series. Biometrika 73: 461–466.
Tsay, R. S. (1989). Testing and modeling threshold autoregressive processes. Journal of the American Statistical Association 84: 231–240.
Tsay, R. S. (1998). Testing and modeling multivariate threshold models. Journal of the American Statistical Association 93: 1188–1202.
Venables, W. N. and Ripley, B. D. (1999). Modern Applied Statistics with S-Plus, 3rd edn. Springer, New York.
Watson, G. S. (1964). Smooth regression analysis. Sankhya Series A 26: 359–372.