9.3 Fundamental Factor Models

Fundamental factor models use observable asset specific fundamentals such as industrial classification, market capitalization, book value, and style classification (growth or value) to construct common factors that explain the excess returns. There are two approaches to fundamental factor models available in the literature. The first approach is proposed by Bar Rosenberg, founder of BARRA Inc., and is referred to as the BARRA approach; see Grinold and Kahn (2000). In contrast to the macroeconomic factor models, this approach treats the observed asset specific fundamentals as the factor betas, , and estimates the factors at each time index t via regression methods. The betas are time invariant, but the realizations evolve over time. The second approach is the Fama–French approach proposed by Fama and French (1992). In this approach, the factor realization fjt for a given specific fundamental is obtained by constructing some hedge portfolio based on the observed fundamental. We briefly discuss the two approaches in the next two sections.

9.3.1 BARRA Factor Model

Assume that the excess returns and, hence, the factor realizations are mean corrected. At each time index t, the factor model in Eq. (9.2) reduces to

9.6

where denotes the (sample) mean-corrected excess returns and, for simplicity in notation, we continue to use as factor realizations. Since is given, the model in Eq. (9.6) is a multiple linear regression with k observations and m unknowns. Because the number of common factors m should be less than the number of assets k, the regression is estimable. However, the regression is not homogeneous because the covariance matrix of is with = Var(ϵit), which depends on the ith asset. Consequently, the factor realization at time index t can be estimated by the weighted least-squares (WLS) method using the standard errors of the specific factors as the weights. The resulting estimate is

9.7

In practice, the covariance matrix is unknown so that we use a two-step procedure to perform the estimation.

In step one, the ordinary least-squares (OLS) method is used at each time index t to obtain a preliminary estimate of as

where the second subscript o is used to denote the OLS estimate. This estimate of factor realization is consistent, but not efficient. The residual of the OLS regression is

Since the residual covariance matrix is time invariant, we can pool the residuals together (for t = 1, … , T) to obtain an estimate of as

In step two, we plug in the estimate to obtain a refined estimate of the factor realization

9.8

where the second subscript g denotes the generalized least-squares (GLS) estimate, which is a sample version of the WLS estimate. The residual of the refined regression is

from which we estimate the residual variance matrix as

Finally, the covariance matrix of the estimated factor realizations is

where

From Eq. (9.6), the covariance matrix of the excess returns under the BARRA approach is

9.3.1.1 Industry Factor Model

For illustration, we consider monthly excess returns of 10 stocks and use industrial classification as the specific asset fundamental. The stocks used are given in Table 9.2 and can be classified into three industrial sectors—namely, financial services, computer and high-tech industry, and other. The sample period is again from January 1990 to December 2003. Under the BARRA framework, there are three common factors representing the three industrial sectors and the betas are indicators for the three industrial sectors; that is,

9.9

with the betas being

9.10

where j = 1, 2, 3 representing the financial, high-tech, and other sectors, respectively. For instance, the beta vector for the IBM stock return is and that for Alcoa stock return is .

Table 9.2 Stocks Used and Their Tick Symbols in Analysis of Industrial Factor Modela

aSample mean and standard deviation of the excess returns are also given. The sample span is from January 1990 to December 2003.

In Eq. (9.9), f1t is the factor realization of the financial services sector, f2t is that of the computer and high-tech sector, and f3t is for the other sector. Because the βij are indicator variables, the OLS estimate of is extremely simple. Indeed, is the vector consisting of the averages of sector excess returns at time t. Specifically,

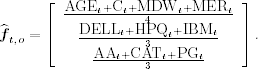
The specific factor of the ith asset is simply the deviation of its excess return from its industrial sample average. One can then obtain an estimate of the residual variance matrix to perform the generalized least-squares estimation. We use S-Plus to perform the analysis. The commands also apply to R. First, load the returns into S-Plus, remove the sample means, create the industrial dummies, and compute the sample correlation matrix of the returns.

The OLS estimates, their residuals, and residual variances are estimated as follows:

One can then obtain the generalized least-squares estimates.

The model-based correlations of stocks within an industrial sector are larger than their sample counterparts. For instance, the sample correlation between CAT and PG stock returns is only 0.1, but the correlation based on the fitted model is 0.6. Finally, Figure 9.3 shows the time plots of the factor realizations based on the generalized least-squares estimation.

Figure 9.3 Estimated factor realizations of BARRA industrial factor model for 10 monthly stock returns in 3 industrial sectors: (a) factor realizations: financial sector, (b) high-tech sector, and (c) other sector.

9.3.1.2 Factor Mimicking Portfolio

Consider the special case of BARRA factor models with a single factor. Here the WLS estimate of ft in Eq. (9.7) has a nice interpretation. Consider a portfolio of the k assets that solves

It turns out that the solution to this portfolio problem is given by

Thus, the estimated factor realization is the portfolio return

If the portfolio is normalized such that = 1, it is referred to as a factor mimicking portfolio. For multiple factors, one can apply the idea to each factor individually.

9.3.2 Fama–French Approach

For a given asset fundamental (e.g., ratio of book-to-market value), Fama and French (1992) determined factor realizations using a two-step procedure. First, they sorted the assets based on the values of the observed fundamental. Then they formed a hedge portfolio, which is long in the top quintile () of the sorted assets and short in the bottom quintile of the sorted assets. The observed return on this hedge portfolio at time t is the observed factor realization for the given asset fundamental. The procedure is repeated for each asset fundamental under consideration. Finally, given the observed factor realizations , the betas for each asset are estimated using a time series regression method. These authors identify three observed fundamentals that explain high percentages of variability in excess returns. The three fundamentals used by Fama and French are (a) the overall market return (market excess return), (b) the performance of small stocks relative to large stocks (SMB, small minus big), and (c) the performance of value stocks relative to growth stocks (HML, high minus low). The size sorted by market equity and the ratio of book equity to market equity is used to define value and growth stocks with value stocks having high book equity to market equity ratio.