3.6 The Integrated GARCH Model
If the AR polynomial of the GARCH representation in Eq. (3.15) has a unit root, then we have an IGARCH model. Thus, IGARCH models are unit-root GARCH models. Similar to ARIMA models, a key feature of IGARCH models is that the impact of past squared shocks ηt−i = 
for i > 0 on 
is persistent.
An IGARCH(1,1) model can be written as
where {ϵt} is defined as before and 1 > β1 > 0. For the monthly excess returns of the S&P 500 index, an estimated IGARCH(1,1) model is
where the standard errors of the estimates in the volatility equation are 0.0017, 0.000013, and 0.0144, respectively. The parameter estimates are close to those of the GARCH(1,1) model shown before, but there is a major difference between the two models. The unconditional variance of at, hence that of rt, is not defined under the above IGARCH(1,1) model. This seems hard to justify for an excess return series. From a theoretical point of view, the IGARCH phenomenon might be caused by occasional level shifts in volatility. The actual cause of persistence in volatility deserves a careful investigation.
When α1 + β1 = 1, repeated substitutions in Eq. (3.17) give
where h is the forecast origin. Consequently, the effect of 
on future volatilities is also persistent, and the volatility forecasts form a straight line with slope α0. Nelson (1990) studies some probability properties of the volatility process 
under an IGARCH model. The process 
is a martingale for which some nice results are available in the literature. Under certain conditions, the volatility process is strictly stationary but not weakly stationary because it does not have the first two moments.
The case of α0 = 0 is of particular interest in studying the IGARCH(1,1) model. In this case, the volatility forecasts are simply 
for all forecast horizons; see Eq. (3.22). This special IGARCH(1,1) model is the volatility model used in RiskMetrics, which is an approach for calculating value at risk; see Chapter 7. The model is also an exponential smoothing model for the 
series. To see this, rewrite the model as
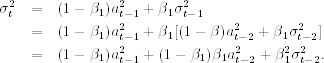
By repeated substitutions, we have
which is the well-known exponential smoothing formation with β1 being the discounting factor. Exponential smoothing methods can thus be used to estimate such an IGARCH(1,1) model.