To better understand cointegration, we focus on VAR models for their simplicity in estimation. Consider a k-dimensional VAR(p) time series 
with possible time trend so that the model is
8.35 
where the innovation 
is assumed to be Gaussian and 
= 
, where 
and 
are k-dimensional constant vectors. Write 
= 
. Recall that if all zeros of the determinant 
are outside the unit circle, then 
is unit-root stationary. In the literature, a unit-root stationary series is said to be an I(0) process; that is, it is not integrated. If 
= 0, then 
is unit-root nonstationary. For simplicity, we assume that 
is at most an integrated process of order 1; that is, an I(1) process. This means that (1 − B)xit is unit-root stationary if xit itself is not.
An error correction model (ECM) for the VAR(p) process 
is
where 
are defined in Eq. (8.34) and 
= 
. We refer to the term 
of Eq. (8.36) as the error correction term, which plays a key role in cointegration study. Notice that 
can be recovered from the ECM representation via
where 
, the zero matrix. Based on the assumption that 
is at most I(1), 
of Eq. (8.36) is an I(0) process.
If 
contains unit roots, then 
= 0 so that 
is singular. Therefore, three cases are of interest in considering the ECM in Eq. (8.36):
1. Rank(
) = 0. This implies 
and 
is not cointegrated. The ECM of Eq. (8.36) reduces to
so that 
follows a VAR(p − 1) model with deterministic trend 
.
2. Rank(
) = k. This implies that 
and 
contains no unit roots; that is, 
is I(0). The ECM model is not informative and one studies 
directly.
3. 
. In this case, one can write 
as
where 
and 
are k × m matrices with Rank(
) = Rank(
) = m. The ECM of Eq. (8.36) becomes
8.38 
This means that 
is cointegrated with m linearly independent cointegrating vectors, 
, and has k − m unit roots that give k − m common stochastic trends of 
.
If 
is cointegrated with Rank(
) = m, then a simple way to obtain a presentation of the k − m common trends is to obtain an orthogonal complement matrix 
of 
; that is, 
is a k × (k − m) matrix such that 
, a (k − m) × m zero matrix, and use 
. To see this, one can premultiply the ECM by 
and use 
to see that there would be no error correction term in the resulting equation. Consequently, the (k − m)-dimensional series 
should have k − m unit roots. For illustration, consider the bivariate example of Section 8.5.1. For this special series, 
and 
. Therefore, 
, which is precisely the unit-root nonstationary series y1t in Eq. (8.32).
Note that the factorization in Eq. (8.37) is not unique because for any m × m orthogonal matrix 
satisfying 
, we have a
where both 
and 
are also of rank m. Additional constraints are needed to uniquely identify 
and 
. It is common to require that 
, where 
is the m × m identity matrix and 
is a (k − m) × m matrix. In practice, this may require reordering of the elements of 
such that the first m components all have a unit root. The elements of 
and 
must also satisfy other constraints for the process 
to be unit-root stationary. For example, consider the case of a bivariate VAR(1) model with one cointegrating vector. Here k = 2, m = 1, and the ECM is
Premultiplying the prior equation by 
, using 
, and moving wt−1 to the right-hand side of the equation, we obtain
where 
. This implies that wt is a stationary AR(1) process. Consequently, αi and β1 must satisfy the stationarity constraint |1 + α1 + α2β1| < 1.
The prior discussion shows that the rank of 
in the ECM of Eq. (8.36) is the number of cointegrating vectors. Thus, to test for cointegration, one can examine the rank of 
. This is the approach taken by Johansen (1988, 1995) and Reinsel and Ahn (1992).
8.6.1 Specification of the Deterministic Function
Similar to the univariate case, the limiting distributions of cointegration tests depend on the deterministic function 
. In this section, we discuss some specifications of 
that have been proposed in the literature. To understand some of the statements made below, keep in mind that 
provides a presentation for the common stochastic trends of 
if it is cointegrated.
1. 
: In this case, all the component series of 
are I(1) without drift and the stationary series 
has mean zero.
2. 
, where 
is an m-dimensional nonzero constant vector. The ECM becomes
so that the components of 
are I(1) without drift, but 
have a nonzero mean 
. This is referred to as the case of restricted constant.
3. 
, which is nonzero. Here the component series of 
are I(1) with drift 
and 
may have a nonzero mean.
4. 
, where 
is a nonzero vector. The ECM becomes
so that the components of 
are I(1) with drift 
and 
has a linear time trend related to 
. This is the case of restricted trend.
5. 
= 
, where 
are nonzero. Here both the constant and trend are unrestricted. The components of 
are I(1) and have a quadratic time trend and 
have a linear trend.
Obviously, the last case is not common in empirical work. The first case is not common for economic time series but may represent the log price series of some assets. The third case is also useful in modeling asset prices.
8.6.2 Maximum-Likelihood Estimation
In this section, we briefly outline the maximum-likelihood estimation (MLE) of a cointegrated VAR(p) model. Suppose that the data are 
. Without loss of generality, we write 
, where 
, and it is understood that 
depends on the specification of the previous section. For a given m, which is the rank of 
, the ECM model becomes
8.39 
where t = p + 1, … , T. A key step in the estimation is to concentrate the likelihood function with respect to the deterministic term and the stationary effects. This is done by considering the following two multivariate linear regressions:
Let 
and 
be the residuals of Eqs. (8.40) and (8.41), respectively. Define the sample covariance matrices
Next, compute the eigenvalues and eigenvectors of 
with respect to 
. This amounts to solving the eigenvalue problem
Denote the eigenvalue and eigenvector pairs by 
, where 
. Here the eigenvectors are normalized so that 
, where 
is the matrix of eigenvectors.
The unnormalized MLE of the cointegrating vector 
is 
and from which we can obtain an MLE for 
that satisfies the identifying constraint and normalization condition. Denote the resulting estimate by 
with the subscript c signifying constraints. The MLE of other parameters can then be obtained by the multivariate linear regression
The maximized value of the likelihood function based on m cointegrating vectors is
This value is used in the maximum-likelihood ratio test for testing Rank(
) = m. Finally, estimates of the orthogonal complements of 
and 
can be obtained using
8.6.3 Cointegration Test
For a specified deterministic term 
, we now discuss the maximum-likelihood test for testing the rank of the 
matrix in Eq. (8.36). Let H(m) be the null hypothesis that the rank of 
is m. For example, under H(0), Rank(
) = 0 so that 
and there is no cointegration. The hypotheses of interest are
For testing purpose, the ECM in Eq. (8.36) becomes
where t = p + 1, … , T. Our goal is to test the rank of 
. Mathematically, the rank of 
is the number of nonzero eigenvalues of 
, which can be obtained if a consistent estimate of 
is available. Based on the prior equation, which is in the form of a multivariate linear regression, we see that 
is related to the covariance matrix between 
and 
after adjusting for the effects of 
and 
for i = 1, … , p − 1. The necessary adjustments can be achieved by the techniques of multivariate linear regression shown in the previous section. Indeed, the adjusted series of 
and 
are 
and 
, respectively. The equation of interest for the cointegration test then becomes
Under the normality assumption, the likelihood ratio test for testing the rank of 
in the prior equation can be done by using the canonical correlation analysis between 
and 
. See Johnson and Wichern (1998) for information on canonical correlation analysis. The associated canonical correlations are the partial canonical correlations between 
and 
because the effects of 
and 
have been adjusted. The quantities 
are the squared canonical correlations between 
and 
.
Consider the hypotheses
Johansen (1988) proposes the likelihood ratio (LR) statistic
8.42 
to perform the test. If Rank(
) = m, then 
should be small for i > m and hence LRtr(m) should be small. This test is referred to as the trace cointegration test. Due the presence of unit roots, the asymptotic distribution of LRtr(m) is not chi squared but a function of standard Brownian motions. Thus, critical values of LRtr(m) must be obtained via simulation.
Johansen (1988) also considers a sequential procedure to determine the number of cointegrating vectors. Specifically, the hypotheses of interest are
The LR ratio test statistic, called the maximum eigenvalue statistic, is
Again, critical values of the test statistics are nonstandard and must be evaluated via simulation.
8.6.4 Forecasting of Cointegrated VAR Models
The fitted ECM can be used to produce forecasts. First, conditioned on the estimated parameters, the ECM equation can be used to produce forecasts of the differenced series 
. Such forecasts can in turn be used to obtain forecasts of 
. A difference between ECM forecasts and the traditional VAR forecasts is that the ECM approach imposes the cointegration relationships in producing the forecasts.
8.6.5 An Example
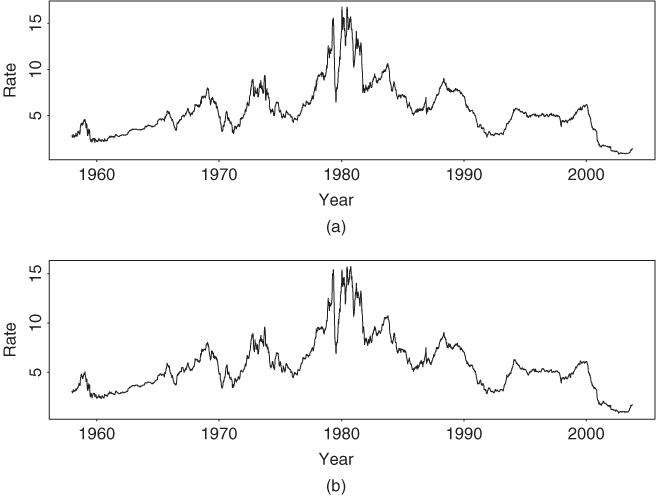
To demonstrate the analysis of cointegrated VAR models, we consider two weekly U.S. short-term interest rates. The series are the 3-month Treasury bill (TB) rate and 6-month Treasury bill rate from December 12, 1958, to August 6, 2004, for 2383 observations. The TB rates are from the secondary market and obtained from the Federal Reserve Bank of St. Loius. Figure 8.12 shows the time plots of the interest rates. As expected, the two series move closely together.
Figure 8.12 Time plots of weekly U.S. interest rate from December 12, 1958, to August 6, 2004. (a) The 3-month Treasury bill rate and (b) 6-month Treasury bill rate. Rates are from secondary market.
Our analysis uses the S-Plus software with commands VAR for VAR analysis, coint for cointegration test, and VECM for vector error correction estimation. Denote the two series by tb3m and tb6m and define the vector series 
. The augmented Dickey–Fuller unit-root tests fail to reject the hypothesis of a unit root in the individual series; see Chapter 2. Indeed, the test statistics are − 2.34 and − 2.33 with p value about 0.16 for the 3-month and 6-month interest rate when an AR(3) model is used. Thus, we proceed to VAR modeling.
For the bivariate series 
, the BIC criterion selects a VAR(3) model:
> x=cbind(tb3m,tb6m)
> y=data.frame(x)
> ord.choice$ar.order
[1] 3
To perform a cointegration test, we choose a restricted constant for 
because there is no reason a priori to believe the existence of a drift in the U.S. interest rate. Both Johansen's tests confirm that the two series are cointegrated with one cointegrating vector when a VAR(3) model is entertained.
> cointst.rc=coint(x,trend=‘rc’, lags=2) % lags = p-1.
> cointst.rc
Call:
coint(Y = x, lags = 2, trend = “rc”)
Trend Specification:
H1*(r): Restricted constant
Trace tests sign. at the 5% level are flagged by ‘ +’.
Trace tests sign. at the 1% level are flagged by ‘++’.
Max Eig. tests sign. at the 5% level are flagged by ‘ *’.
Max Eig. tests sign. at the 1% level are flagged by ‘**’.
Tests for Cointegration Rank:
Eigenvalue Trace Stat 95% CV 99% CV
H(0)++** 0.0322 83.2712 19.96 24.60
H(1) 0.0023 5.4936 9.24 12.97
Max Stat 95% CV 99% CV
H(0)++** 77.7776 15.67 20.20
H(1) 5.4936 9.24 12.97
Next, we perform the maximum-likelihood estimation of the specified cointegrated VAR(3) model using an ECM presentation. The results are as follows:
> vecm.fit=VECM(cointst.rc)
> summary(vecm.fit)
Call:
VECM(test = cointst.rc)
Cointegrating Vectors:
coint.1
1.0000
tb6m −1.0124
(std.err) 0.0086
(t.stat) −118.2799
Intercept* 0.2254
(std.err) 0.0545
(t.stat) 4.1382
VECM Coefficients:
tb3m tb6m
coint.1 −0.0949 −0.0211
(std.err) 0.0199 0.0179
(t.stat) −4.7590 −1.1775
tb3m.lag1 0.0466 −0.0419
(std.err) 0.0480 0.0432
(t.stat) 0.9696 −0.9699
tb6m.lag1 0.2650 0.3164
(std.err) 0.0538 0.0484
(t.stat) 4.9263 6.5385
tb3m.lag2 −0.2067 −0.0346
(std.err) 0.0481 0.0433
(t.stat) −4.2984 −0.8005
tb6m.lag2 0.2547 0.0994
(std.err) 0.0543 0.0488
(t.stat) 4.6936 2.0356
Regression Diagnostics:
tb3m tb6m
R-squared 0.1081 0.0913
Adj. R-squared 0.1066 0.0898
Resid. Scale 0.2009 0.1807
> plot(vecm.fit)
Make a plot selection (or 0 to exit):
1: plot: All
2: plot: Response and Fitted Values
3: plot: Residuals
...
13: plot: PACF of Squared Cointegrating Residuals
Selection:
As expected, the output shows that the stationary series is wt ≈ tb3mt − tb6mt and the mean of wt is about − 0.225. The fitted ECM is
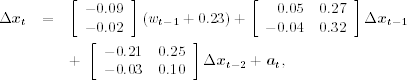
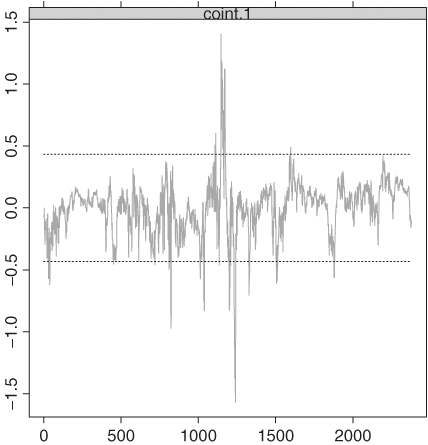
and the estimated standard errors of ait are 0.20 and 0.18, respectively. Adequacy of the fitted ECM can be examined via various plots. For illustration, Figure 8.13 shows the cointegrating residuals. Some large residuals are shown in the plot, which occurred in the early 1980s when the interest rates were high and volatile.
Figure 8.13 Time plot of cointegrating residuals for an ECM fit to weekly U.S. interest rate series. Data span is from December 12, 1958, to August 6, 2004.
Finally, we use the fitted ECM to produce 1-step- to 10-step-ahead forecasts for both 
and 
. The forecast origin is August 6, 2004.
> vecm.fst=predict(vecm.fit, n.predict=10)
> summary(vecm.fst)
Predicted Values with Standard Errors:
tb3m tb6m
1-step-ahead −0.0378 −0.0642
(std.err) 0.2009 0.1807
2-step-ahead −0.0870 −0.0864
(std.err) 0.3222 0.2927
...
10-step-ahead −0.2276 −0.1314
(std.err) 0.8460 0.8157
> plot(vecm.fst,xold=diff(x),n.old=12)
> vecm.fit.level=VECM(cointst.rc,levels=T)
> vecm.fst.level=predict(vecm.fit.level, n.predict=10)
> summary(vecm.fst.level)
Predicted Values with Standard Errors:
tb3m tb6m
1-step-ahead 1.4501 1.7057
(std.err) 0.2009 0.1807
2-step-ahead 1.4420 1.7017
(std.err) 0.3222 0.2927
...
10-step-ahead 1.4722 1.7078
(std.err) 0.8460 0.8157
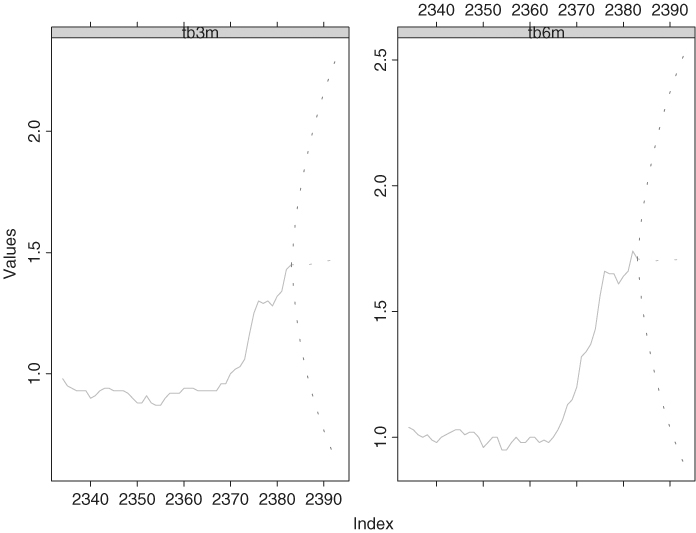
> plot(vecm.fst.level, xold=x, n.old=50)
The forecasts are shown in Figures 8.14 and 8.15 for the differenced data and the original series, respectively, along with some observed data points. The dashed lines in the plots are pointwise 95% confidence intervals. Because of unit-root nonstationarity, the intervals are wide and not informative.
Figure 8.14 Forecasting plots of fitted ECM model for weekly U.S. interest rate series. Forecasts are for differenced series and forecast origin is August 6, 2004.
Figure 8.15 Forecasting plots of fitted ECM model for weekly U.S. interest rate series. Forecasts are for interest rates and forecast origin is August 6, 2004.
Remark
The package urca of R can be used to perform Johansen's co-integration test. The command is ca.jo. It requires specification of some subcommands. See the section of pairs trading for demonstration.