Conditional distributions play a key role in Gibbs sampling. In the statistical literature, these conditional distributions are referred to as conditional posterior distributions because they are distributions of parameters given the data, other parameter values, and the entertained model. In this section, we review some well-known posterior distributions that are useful in using MCMC methods.
12.3.1 Posterior Distributions
There are two approaches to statistical inference. The first approach is the classical approach based on the maximum-likelihood principle. Here a model is estimated by maximizing the likelihood function of the data, and the fitted model is used to make inference. The other approach is Bayesian inference that combines prior belief with data to obtain posterior distributions on which statistical inference is based. Historically, there were heated debates between the two schools of statistical inference. Yet both approaches have proved to be useful and are now widely accepted. The methods discussed so far in this book belong to the classical approach. However, Bayesian solutions exist for all of the problems considered. This is particularly so in recent years with the advances in MCMC methods, which greatly improve the feasibility of Bayesian analysis. Readers can revisit the previous chapters and derive MCMC solutions for the problems considered. In most cases, the Bayesian solutions are similar to what we had before. In some cases, the Bayesian solutions might be advantageous. For example, consider the calculation of value at risk in Chapter 7. A Bayesian solution can easily take into consideration the parameter uncertainty in VaR calculation. However, the approach requires intensive computation.
Let 
be the vector of unknown parameters of an entertained model and X be the data. Bayesian analysis seeks to combine knowledge about the parameters with the data to make inference. Knowledge of the parameters is expressed by specifying a prior distribution for the parameters, which is denoted by 
. For a given model, denote the likelihood function of the data by . Then by the definition of conditional probability,
where the marginal distribution f(X) can be obtained by
The distribution f(
|X) in Eq. (12.4) is called the posterior distribution of 
. In general, we can use Bayes's rule to obtain
where 
is the prior distribution and f(X|) is the likelihood function. From Eq. (12.5), making statistical inference based on the likelihood function f(X|) amounts to using a Bayesian approach with a constant prior distribution.
12.3.2 Conjugate Prior Distributions
Obtaining the posterior distribution in Eq. (12.4) is not simple in general, but there are cases in which the prior and posterior distributions belong to the same family of distributions. Such a prior distribution is called a conjugate prior distribution. For MCMC methods, use of conjugate priors means that a closed-form solution for the conditional posterior distributions is available. Random draws of the Gibbs sampler can then be obtained by using the commonly available computer routines of probability distributions. In what follows, we review some well-known conjugate priors. For more information, readers are referred to textbooks on Bayesian statistics (e.g., DeGroot 1970, Chapter 9).
Result 12.1
Suppose that x1, … , xn form a random sample from a normal distribution with mean μ, which is unknown, and variance σ2, which is known and positive. Suppose that the prior distribution of μ is a normal distribution with mean μo and variance 
. Then the posterior distribution of μ given the data and prior is normal with mean μ* and variance 
given by
where 
is the sample mean.
In Bayesian analysis, it is often convenient to use the precision parameter η = 1/σ2 (i.e., the inverse of the variance σ2). Denote the precision parameter of the prior distribution by and that of the posterior distribution by 
. Then Result 12.1 can be rewritten as
For the normal random sample considered, data information about μ is contained in the sample mean 
, which is the sufficient statistic of μ. The precision of 
is n/σ2 = nη. Consequently, Result 12.1 says that (a) precision of the posterior distribution is the sum of the precisions of the prior and the data, and (b) the posterior mean is a weighted average of the prior mean and sample mean with weight proportional to the precision. The two formulas also show that the contribution of the prior distribution is diminishing as the sample size n increases.
A multivariate version of Result 12.1 is particularly useful in MCMC methods when linear regression models are involved; see Box and Tiao (1973).
Result 12.1a
Suppose that x1, …, xn form a random sample from a multivariate normal distribution with mean vector μ and a known covariance matrix Σ. Suppose also that the prior distribution of μ is multivariate normal with mean vector μo and covariance matrix Σo. Then the posterior distribution of μ is also multivariate normal with mean vector μ* and covariance matrix Σ*, where
where 
is the sample mean, which is distributed as a multivariate normal with mean μ and covariance matrix Σ/n. Note that nΣ−1 is the precision matrix of 
and 
is the precision matrix of the prior distribution.
A random variable η has a gamma distribution with positive parameters α and β if its probability density function is
where Γ(α) is a gamma function. For this distribution, E(η) = α/β and Var(η) =
α/β2.
Result 12.2
Suppose that x1, … , xn form a random sample from a normal distribution with a given mean μ and an unknown precision η. If the prior distribution of η is a gamma distribution with positive parameters α and β, then the posterior distribution of η is a gamma distribution with parameters α + (n/2) and 
.
A random variable θ has a beta distribution with positive parameters α and β if its probability density function is
The mean and variance of θ are E(θ) = α/(α + β) and Var(θ) = αβ/[(α + β)2(α + β + 1)].
Result 12.3
Suppose that x1, … , xn form a random sample from a Bernoulli distribution with parameter θ. If the prior distribution of θ is a beta distribution with given positive parameters α and β, then the posterior of θ is a beta distribution with parameters 
and 
.
Result 12.4
Suppose that x1, … , xn form a random sample from a Poisson distribution with parameter λ. Suppose also that the prior distribution of λ is a gamma distribution with given positive parameters α and β. Then the posterior distribution of λ is a gamma distribution with parameters 
and β + n.
Result 12.5
Suppose that x1, … , xn form a random sample from an exponential distribution with parameter λ. If the prior distribution of λ is a gamma distribution with given positive parameters α and β, then the posterior distribution of λ is a gamma distribution with parameters α + n and 
.
A random variable X has a negative binomial distribution with parameters m and λ, where m > 0 and 0 < λ < 1, if X has a probability mass function
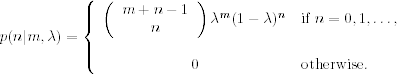
A simple example of negative binomial distribution in finance is how many MBA graduates a firm must interview before finding exactly m “right candidates” for its m openings, assuming that the applicants are independent and each applicant has a probability λ of being a perfect fit. Denote the total number of interviews by Y. Then X = Y − m is distributed as a negative binomial with parameters m and λ.
Result 12.6
Suppose that x1, … , xn form a random sample from a negative binomial distribution with parameters m and λ, where m is positive and fixed. If the prior distribution of λ is a beta distribution with positive parameters α and β, then the posterior distribution of λ is a beta distribution with parameters α + mn and 
.
Next we consider the case of a normal distribution with an unknown mean μ and an unknown precision η. The two-dimensional prior distribution is partitioned as P(μ, η) = P(μ|η)P(η).
Result 12.7
Suppose that x1, … , xn form a random sample from a normal distribution with an unknown mean μ and an unknown precision η. Suppose also that the conditional distribution of μ given η = ηo is a normal distribution with mean μo and precision τoηo and the marginal distribution of η is a gamma distribution with positive parameters α and β. Then the conditional posterior distribution of μ given η = ηo is a normal distribution with mean μ* and precision η*,
where 
is the sample mean, and the marginal posterior distribution of η is a gamma distribution with parameters α + (n/2) and β*, where
When the conditional variance of a random variable is of interest, an inverted chi-squared distribution (or inverse chi-squared) is often used. A random variable Y has an inverted chi-squared distribution with v degrees of freedom if 1/Y follows a chi-squared distribution with the same degrees of freedom. The probability density function of Y is
For this distribution, we have E(Y) = 1/(v − 2) if v > 2 and Var(Y) = 2/[(v − 2)2(v − 4)] if v > 4.
Result 12.8
Suppose that a1, … , an form a random sample from a normal distribution with mean zero and variance σ2. Suppose also that the prior distribution of σ2 is an inverted chi-squared distribution with v degrees of freedom [i.e., 
, where λ > 0]. Then the posterior distribution of σ2 is also an inverted chi-squared distribution with v + n degrees of freedom—that is, 
.