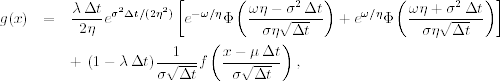Empirical studies have found that the stochastic diffusion model based on Brownian motion fails to explain some characteristics of asset returns and the prices of their derivatives [e.g., the “volatility smile” of implied volatilities; see Bakshi, Cao, and Chen (1997) and the references therein]. Volatility smile is referred to as the convex function between the implied volatility and strike price of an option. Both out-of-the-money and in-the-money options tend to have higher implied volatilities than at-the-money options especially in the foreign exchange markets. Volatility smile is less pronounced for equity options. The inadequacy of the standard stochastic diffusion model has led to the developments of alternative continuous-time models. For example, jump diffusion and stochastic volatility models have been proposed in the literature to overcome the inadequacy; see Merton (1976) and Duffie (1995).
Jumps in stock prices are often assumed to follow a probability law. For example, the jumps may follow a Poisson process, which is a continuous-time discrete process. For a given time t, let Xt be the number of times a special event occurs during the time period [0, t]. Then Xt is a Poisson process if
That is, Xt follows a Poisson distribution with parameter λt. The parameter λ governs the occurrence of the special event and is referred to as the rate or intensity of the process. A formal definition also requires that Xt be a right-continuous homogeneous Markov process with left-hand limit.
In this section, we discuss a simple jump diffusion model proposed by Kou (2002). This simple model enjoys several nice properties. The returns implied by the model are leptokurtic and asymmetric with respect to zero. In addition, the model can reproduce volatility smile and provide analytical formulas for the prices of many options. The model consists of two parts, with the first part being continuous and following a geometric Brownian motion and the second part being a jump process. The occurrences of jump are governed by a Poisson process, and the jump size follows a double exponential distribution. Let Pt be the price of an asset at time t. The simple jump diffusion model postulates that the price follows the stochastic differential equation
where wt is a Wiener process, nt is a Poisson process with rate λ, and {Ji} is a sequence of independent and identically distributed nonnegative random variables such that X = ln(J) has a double exponential distribution with probability density function
The double exponential distribution is also referred to as the Laplacian distribution. In model (6.26), nt, wt, and Ji are independent so that there is no relation between the randomness of the model. Notice that nt is the number of jumps in the time interval [0, t] and follows a Poisson distribution with parameter λt, where λ is a constant. At the ith jump, the proportion of price jump is Ji − 1.
The double exponential distribution can be written as
where ξ is an exponential random variable with mean η and variance η2. The probability density function of ξ is
Some useful properties of the double exponential distribution are
For finite samples, it is hard to distinguish a double exponential distribution from a Student-t distribution. However, a double exponential distribution is more tractable analytically and can generate a higher probability concentration (e.g., higher peak) around its mean value. As stated in Chapter 1, histograms of observed asset returns tend to have a higher peak than the normal density. Figure 6.8 shows the probability density function of a double exponential random variable in the solid line and that of a normal random variable in the dotted line. Both variables have mean zero and variance 0.0008. The high peak of the double exponential density is clearly seen.
Figure 6.8 Probability density functions of double exponential and normal random variable with mean zero and variance 0.0008. Solid line denotes the double exponential distribution. Dotted line is the normal distribution.
Solving the stochastic differential equation in Eq. (6.26), we obtain the dynamics of the asset price as
where it is understood that 
. This result is a generalization of Eq. (6.25) by including the stochastic jumps. It can be obtained as follows. Let ti be the time of the ith jump. For t ∈ [0, t1), there is no jump and the price is given in Eq. (6.25). Consequently, the left-hand price limit at time t1 is
At time t1, the proportion of price jump is J1 − 1 so that the price becomes
For t ∈ (t1, t2), there is no jump in the interval (t1, t] so that
Plugging in 
, we have
Repeating the scheme, we obtain Eq. (6.29).
From Eq. (6.29), the simple return of the underlying asset in a small time increment Δt becomes
where it is understood that a summation over an empty set is zero and Xi = ln(Ji). For a small Δt, we may use the approximation ex ≈ 1 + x + x2/2 and the result (Δwt)2 ≈ Δt discussed in Section 6.3 to obtain
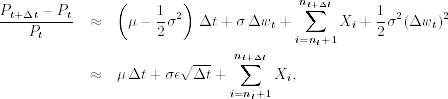
where Δwt = wt+Δt − wt and ϵ is a standard normal random variable.
Under the assumption of a Poisson process, the probability of having one jump in the time interval (t, t + Δt] is λ Δt and that of having more than one jump is o(Δt), where the symbol o(Δt) means that if we divide this term by Δt then its value tends to zero as Δt tends to zero. Therefore, for a small Δt, by ignoring multiple jumps, we have
Combining the prior results, we see that the simple return of the underlying asset is approximately distributed as
where I is a Bernoulli random variable with Pr(I = 1) = λ Δt and Pr(I = 0) = 1 − λ Δt, and X is a double exponential random variable defined in Eq. (6.28). Equation (6.30) reduces to that of a geometric Brownian motion without jumps.
Let 
be the random variable on the right-hand side of Eq. (6.30). Using the independence between the exponential and normal distributions used in the model, Kou (2002) obtains the probability density function of G as
where ω = x − μ Δt − κ, and f( · ) and Φ( · ) are, respectively, the probability density and cumulative distribution functions of the standard normal random variable. Furthermore,
Figure 6.9 shows some comparisons between probability density functions of a normal distribution and the distribution of Eq. (6.31). Both distributions have mean zero and variance 2.0572 × 10−4. The mean and variance are obtained by assuming that the return of the underlying asset satisfies μ = 20% per annum, σ = 20% per annum, Δt = 1 day = 1/252 year, λ = 10, κ = − 0.02, and η = 0.02. In other words, we assume that there are about 10 daily jumps per year with average jump size − 2%, and the jump size standard error is 2%. These values are reasonable for a U.S. stock. From the plots, the leptokurtic feature of the distribution derived from the jump diffusion process in Eq. (6.26) is clearly shown. The distribution has a higher peak and fatter tails than the corresponding normal distribution.
Figure 6.9 Density comparisons between normal distribution and distribution of Eq. (6.31). Dotted line denotes the normal distribution. Both distributions have mean zero and variance 2.0572 × 10−4. (a) Overall comparison, (b) comparison of peaks, (c) left tails, and (d) right tails.
6.9.1 Option Pricing under Jump Diffusion
In the presence of random jumps, the market becomes incomplete. In this case, the standard hedging arguments are not applicable to price an option. But we can still derive an option pricing formula that does not depend on attitudes toward risk by assuming that the number of securities available is very large so that the risk of the sudden jumps is diversifiable and the market will therefore pay no risk premium over the risk-free rate for bearing this risk. Alternatively, for a given set of risk premiums, one can consider a risk-neutral measure P* such that
where r is the risk-free interest rate, J = exp(X) such that X follows the double exponential distribution of Eq. (6.27), ψ = eκ/(1 − η2) − 1, 0 < η < 1, and the parameters κ, η, ψ, and σ become risk-neutral parameters taking consideration of the risk premiums; see Kou (2002) for more details. The unique solution of the prior equation is given by
To price a European option in the jump diffusion model, it remains to compute the expectation, under the measure P*, of the discounted final payoff of the option. In particular, the price of a European call option at time t is given by
(6.32)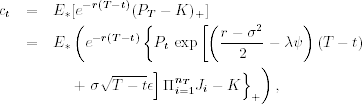 
where T is the expiration time, (T − t) is the time to expiration measured in years, K is the strike price, (y)+ = max(0, y), and ϵ is a standard normal random variable. Kou (2002) shows that ct is analytically tractable as
where Φ( · ) is the CDF of the standard normal random variable,
and the Hhi( · ) functions are defined as
(6.34) 
and Hh−1(x) = exp( − x2/2), which is 
with f(x) being the probability density function of a standard normal random variable; see Abramowitz and Stegun (1972). The Hhn(x) functions satisfy the recursion
(6.35) 
with starting values 
and 
.
The pricing formula involves an infinite series, but its numerical value can be approximated quickly and accurately through truncation (e.g., the first 10 terms). Also, if λ = 0 (i.e., there are no jumps), then it is easily seen that ct reduces to the Black–Scholes formula for a call option discussed before.
Finally, the price of a European put option under the jump diffusion model considered can be obtained by using the putf-call parity; that is,
Pricing formulas for other options under the jump diffusion model in Eq. (6.26) can be found in Kou (2002).
Example 6.8
Consider the stock of Example 6.6, which has a current price of $80. As before, assume that the strike price of a European option is K = $81 and other parameters are r = 0.08 and T − t = 0.25. In addition, assume that the price of the stock follows the jump diffusion model in Eq. (6.26) with parameters λ = 10, κ = − 0.02, and η = 0.02. In other words, there are about 10 jumps per year with average jump size − 2% and jump size standard error of 2%. Using the formula in Eq. (6.33), we obtain ct = $3.92, which is higher than the $3.49 of Example 6.6 when there are no jumps. The corresponding put option assumes the value pt = $3.31, which is also higher than what we had before. As expected, adding the jumps while keeping the other parameters fixed increases the prices of both European options. Keep in mind, however, that adding the jump process to the stock price in a real application often leads to different estimates for the stock volatility σ.