Appendix A: Review of Vectors and Matrices

In this appendix, we briefly review some algebra and properties of vectors and matrices. No proofs are given as they can be found in standard textbooks on matrices (e.g., Graybill, 1969).

An m × n real-valued matrix is an m × n array of real numbers. For example,

is a 2 × 3 matrix. This matrix has two rows and three columns. In general, an m × n matrix is written as

8.46

The positive integers m and n are the row dimension and column dimension of . The real number aij is referred to as the (i, j)th element of . In particular, the elements aii are the diagonal elements of the matrix.

An m × 1 matrix forms an m-dimensional column vector, and a 1 × n matrix is an n-dimensional row vector. In the literature, a vector is often meant to be a column vector. If m = n, then the matrix is a square matrix. If aij = 0 for i ≠ j and m = n, then the matrix is a diagonal matrix. If aij = 0 for i ≠ j and aii = 1 for all i, then is the m × m identity matrix, which is commonly denoted by or simply if the dimension is clear.

The n × m matrix

is the transpose of the matrix . For example,

We use the notation = to denote the transpose of . From the definition, and = . If = , then is a symmetric matrix.

Basic Operations

Suppose that and are two matrices with dimensions given in the subscript. Let b be a real number. Some basic matrix operations are defined next:

• Addition: 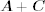= [aij + cij]m×n if m = p and n = q.
• Subtraction: 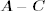= [aij − cij]m×n if m = p and n = q.
• Scalar multiplication: .
• Multiplication: provided that n = p.

When the dimensions of matrices satisfy the condition for multiplication to take place, the two matrices are said to be conformable. An example of matrix multiplication is

Important rules of matrix operations include (a) and (b) in general.

Inverse, Trace, Eigenvalue, and Eigenvector

A square matrix is nonsingular or invertible if there exists a unique matrix such that = = , the m × m identity matrix. In this case, is called the inverse matrix of and is denoted by = .

The trace of is the sum of its diagonal elements [i.e., ]. It is easy to see that (a) , (b) , and (c) provided that the two matrices are conformable.

A number λ and an m × 1 vector , possibly complex valued, are a right eigenvalue and eigenvector pair of the matrix if . There are m possible eigenvalues for the matrix . For a real-valued matrix , complex eigenvalues occur in conjugated pairs. The matrix is nonsingular if and only if all of its eigenvalues are nonzero. Denote the eigenvalues by {λi|i = 1, … , m}: We have . In addition, the determinant of the matrix can be defined as . For a general definition of determinant of a matrix, see a standard textbook on matrices (e.g., Graybill, 1969).

Finally, the rank of the matrix is the number of nonzero eigenvalues of the symmetric matrix . Also, for a nonsingular matrix , .

Positive-Definite Matrix

A square matrix (m × m) is a positive-definite matrix if (a) is symmetric and (b) all eigenvalues of are positive. Alternatively, is a positive-definite matrix if for any nonzero m-dimensional vector , we have .

Useful properties of a positive-definite matrix include (a) all eigenvalues of are real and positive, and (b) the matrix can be decomposed as

where is a diagonal matrix consisting of all eigenvalues of and is an m × m matrix consisting of the m right eigenvectors of . It is common to write the eigenvalues as λ1 ≥ λ2 ≥ ⋯ ≥ λm and the eigenvectors as such that and . In addition, these eigenvectors are orthogonal to each other—namely, = 0 if i ≠ j—if the eigenvalues are distinct. The matrix is an orthogonal matrix and the decomposition is referred to as the spectral decomposition of the matrix . Consider, for example, the simple 2 × 2 matrix

which is positive definite. Simple calculations show that

Therefore, 3 and 1 are eigenvalues of with normalized eigenvectors and , respectively. It is easy to verify that the spectral decomposition holds—that is,

For a symmetric matrix , there exists a lower triangular matrix with diagonal elements being 1 and a diagonal matrix such that ; see Chapter 1 of Strang (1980). If is positive definite, then the diagonal elements of are positive. In this case, we have

where is again a lower triangular matrix and the square root is taken element by element. Such a decomposition is called the Cholesky decomposition of . This decomposition shows that a positive-definite matrix can be diagonalized as

Since is a lower triangular matrix with unit diagonal elements, is also lower triangular matrix with unit diagonal elements. Consider again the prior 2 × 2 matrix . It is easy to verify that

satisfy . In addition,

Vectorization and Kronecker Product

Writing an m × n matrix in its columns as , we define the stacking operation as vec() = , which is an mn × 1 vector. For two matrices and , the Kronecker product between and is

For example, assume that

Then vec() = (2, − 1, 1, 3)′, vec() = (4, − 2, − 1, 5, 3, 2)′, and

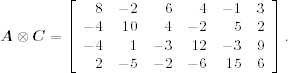
Assuming that the dimensions are appropriate, we have the following useful properties for the two operators:

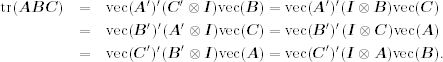
In multivariate statistical analysis, we often deal with symmetric matrices. It is therefore convenient to generalize the stacking operation to the half-stacking operation, which consists of elements on or below the main diagonal. Specifically, for a symmetric square matrix , define

where is the first column of , and is a (k − i + 1)-dimensional vector. The dimension of vech() is k(k + 1)/2. For example, suppose that k = 3. Then we have vech() = (a11, a21, a31, a22, a32, a33)′, which is a six-dimensional vector.