12.6 Missing Values and Outliers

In this section, we discuss MCMC methods for handling missing values and detecting additive outliers. Let be an observed time series. A data point yh is an additive outlier if

12.14

where ω is the magnitude of the outlier and xt is an outlier-free time series. Examples of additive outliers include recording errors (e.g., typos and measurement errors). Outliers can seriously affect time series analysis because they may induce substantial biases in parameter estimation and lead to model misspecification.

Consider a time series xt and a fixed time index h. We can learn a lot about xh by treating it as a missing value. If the model of xt were known, then we could derive the conditional distribution of xh given the other values of the series. By comparing the observed value yh with the derived distribution of xh, we can determine whether yh can be classified as an additive outlier. Specifically, if yh is a value that is likely to occur under the derived distribution, then yh is not an additive outlier. However, if the chance to observe yh is very small under the derived distribution, then yh can be classified as an additive outlier. Therefore, detection of additive outliers and treatment of missing values in time series analysis are based on the same idea.

In the literature, missing values in a time series can be handled by using either the Kalman filter or MCMC methods; see Jones (1980), Chapter 11, and McCulloch and Tsay (1994a). Outlier detection has also been carefully investigated; see Chang, Tiao, and Chen (1988), Tsay (1988), Tsay, Peña, and Pankratz (2000), and the references therein. The outliers are classified into four categories depending on the nature of their impacts on the time series. Here we focus on additive outliers.

12.6.1 Missing Values

For ease in presentation, consider an AR(p) time series

12.15

where {at} is a Gaussian white noise series with mean zero and variance σ2. Suppose that the sampling period is from t = 1 to t = n, but the observation xh is missing, where 1 < h < n. Our goal is to estimate the model in the presence of a missing value.

In this particular instance, the parameters are , where . Thus, we treat the missing value xh as an unknown parameter. If we assume that the prior distributions are

where the hyperparameters are known, then the conditional posterior distributions and are exactly as those given in the previous section, where X denotes the observed data. The conditional posterior distribution is univariate normal with mean μ* and variance . These two parameters can be obtained by using a linear regression model. Specifically, given the model and the data, xh is only related to {xh−p, … , xh−1, xh+1, … , xh+p}. Keeping in mind that xh is an unknown parameter, we can write the relationship as follows:

Consequently, for an AR(p) model, the missing value xh is related to the model, and the data in p + 1 equations

12.16

where ϕ0 = 1. Since a normal distribution is symmetric with respect to its mean, ah and − ah have the same distribution. Consequently, Eq. (12.16) is a special simple linear regression model with p + 1 data points. The least-squares estimate of xh and its variance are

For instance, when p = 1, we have , which is referred to as the filtered value of xh. Because a Gaussian AR(1) model is time reversible, equal weights are applied to the two neighboring observations of xh to obtain the filtered value.

Finally, using Result 12.1, we obtain that the posterior distribution of xh is normal with mean μ* and variance , where

12.17

Missing values may occur in patches, resulting in the situation of multiple consecutive missing values. These missing values can be handled in two ways. First, we can generalize the prior method directly to obtain a solution for multiple filtered values. Consider, for instance, the case that xh and xh+1 are missing. These missing values are related to {xh−p, … , xh−1;xh+2, … , xh+p+1}. We can define a dependent variable yh+j in a similar manner as before to set up a multiple linear regression with parameters xh and xh+1. The least-squares method is then used to obtain estimates of xh and xh+1. Combining with the specified prior distributions, we have a bivariate normal posterior distribution for (xh, xh+1)′. In Gibbs sampling, this approach draws the consecutive missing values jointly. Second, we can apply the result of a single missing value in Eq. (12.17) multiple times within a Gibbs iteration. Again consider the case of missing xh and xh+1. We can employ the conditional posterior distributions and separately. In Gibbs sampling, this means that we draw the missing value one at a time.

Because xh and xh+1 are correlated in a time series, drawing them jointly is preferred in a Gibbs sampling. This is particularly so if the number of consecutive missing values is large. Drawing one missing value at a time works well if the number of missing values is small.

12.6.2 Outlier Detection

Detection of additive outliers in Eq. (12.14) becomes straightforward under the MCMC framework. Except for the case of a patch of additive outliers with similar magnitudes, the simple Gibbs sampler of McCulloch and Tsay (1994a) seems to work well; see Justel, Peña, and Tsay (2001). Again we use an AR model to illustrate the problem. The method applies equally well to other time series models when the Metropolis–Hasting algorithm or the Griddy Gibbs is used to draw values of nonlinear parameters.

Assume that the observed time series is yt, which may contain some additive outliers whose locations and magnitudes are unknown. We write the model for yt as

12.18

where {δt} is a sequence of independent Bernoulli random variables such that P(δt = 1) = ϵ and P(δt = 0) = 1 − ϵ, ϵ is a constant between 0 and 1, {βt} is a sequence of independent random variables from a given distribution, and xt is an outlier-free AR(p) time series,

where {at} is a Gaussian white noise with mean zero and variance σ2. This model seems complicated, but it allows additive outliers to occur at every time point. The chance of being an outlier for each observation is ϵ.

Under the model in Eq. (12.18), we have n data points, but there are 2n + p + 3 parameters—namely, , , , σ2, and ϵ. The binary parameters δt are governed by ϵ and the βt are determined by the specified distribution. The parameters δ and β are introduced by using the idea of data augmentation with δt denoting the presence or absence of an additive outlier at time t, and βt is the magnitude of the outlier at time t when it is present.

Assume that the prior distributions are

where the hyperparameters are known. These are conjugate prior distributions. To implement Gibbs sampling for model estimation with outlier detection, we need to consider the conditional posterior distributions of

where 1 ≤ h ≤ n, Y denotes the data, and θ−1 denotes that the ith element of θ is removed.

Conditioned on δ and β, the outlier-free time series xt can be obtained by xt = yt − δtβt. Information of the data about is then contained in the least-squares estimate

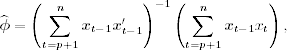
where , which is normally distributed with mean and covariance matrix

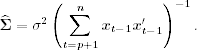
The conditional posterior distribution of is therefore multivariate normal with mean and covariance matrix , which are given in Eq. (12.9) with being replaced by and by . Similarly, the conditional posterior distribution of σ2 is an inverted chi-squared distribution—that is,

where and xt = yt − δtβt.

The conditional posterior distribution of δh can be obtained as follows. First, δh is only related to, with j ≠ h, , and σ2. More specifically, we have

Second, xh can assume two possible values: xh = yh − βh if δh = 1 and xh = yh, otherwise. Define

where if j ≠ h and . The two possible values of xh give rise to two situations:

• Case I: δh = 0. Here the hth observation is not an outlier and 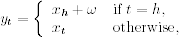. Hence, wj = aj for j = h, … , h + p. In other words, we have

• Case II: δh = 1. Now the hth observation is an outlier and . The wj defined before is contaminated by βh. In fact, we have

Based on the prior discussion, we can summarize the situation as follows:

Since there are n data points, j cannot be greater than n. Let m = min(n, h + p). The posterior distribution of δh is therefore

12.19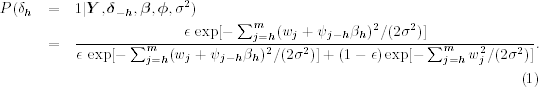

This posterior distribution is simply to compare the weighted values of the likelihood function under the two situations with weight being the probability of each situation.

Finally, the posterior distribution of βh is as follows.

• If δh = 0, then yh is not an outlier and βh ∼ N(0, ξ2).
• If δh = 1, then yh is contaminated by an outlier with magnitude βh. The variable wj defined before contains information of βh for j = h, h + 1, … , min(h + p, n). Specifically, we have wj ∼ N(− ψj−hβh, σ2) for j = h, h + 1, … , min(h + p, n). The information can be put in a linear regression framework as

Example 12.2

Consider the weekly change series of U.S. 3-year Treasury constant maturity interest rate from March 18, 1988, to September 10, 1999, for 600 observations. The interest rate is in percentage and is a subseries of the dependent variable c3t of Example 12.1. The time series is shown in Figure 12.3(a). If AR models are entertained for the series, the partial autocorrelation function suggests an AR(3) model and we obtain

where standard errors of the coefficients are 0.041, 0.042, and 0.041, respectively. The Ljung–Box statistics of the residuals show Q(12) = 11.4, which is insignificant at the 5% level.

Figure 12.3 Time plots of weekly change series of U.S. 3-year Treasury constant maturity interest rate from March 18, 1988, to September 10, 1999: (a) data, (b) posterior probability of being an outlier, and (c) posterior mean of outlier size. Estimation is based on Gibbs sampling with 1050 iterations with first 50 iterations as burn-ins.

Next, we apply the Gibbs sampling to estimate the AR(3) model and to detect simultaneously possible additive outliers. The prior distributions used are

where and . The expected number of additive outliers is 5%. Using initial values ϵ = 0.05, σ2 = 0.012, ϕ1 = 0.2, ϕ2 = 0.02, and ϕ3 = 0.1, we run the Gibbs sampling for 1050 iterations but discard results of the first 50 iterations. Using posterior means of the coefficients as parameter estimates, we obtain the fitted model

where posterior standard deviations of the parameters are 0.046, 0.045, 0.046, and 0.0008, respectively. Thus, the Gibbs sampling produces results similar to that of the maximum-likelihood method. Figure 12.3(b) shows the time plot of posterior probability of each observation being an additive outlier, and Figure 12.3(c) plots the posterior mean of outlier magnitude. From the probability plot, some observations have high probabilities of being an outlier. In particular, t = 323 has a probability of 0.83 and the associated posterior mean of outlier magnitude is − 0.304. This point corresponds to May 20, 1994, when the c3t changed from 0.24 to − 0.34 (i.e., about a 0.6% drop in the weekly interest rate within 2 weeks). The point with second highest posterior probability of being an outlier is t = 201, which is January 17, 1992. The outlying posterior probability is 0.58 and the estimated outlier size is 0.176. At this particular time point, c3t changed from − 0.02 to 0.33, corresponding to a jump of about 0.35% in the weekly interest rate.