In this section, we discuss two alternative methods to volatility modeling.
3.15.1 Use of High-Frequency Data
French, Schwert, and Stambaugh (1987) consider an alternative approach for volatility estimation that uses high-frequency data to calculate volatility of low-frequency returns. In recent years, this approach has attracted substantial interest due to the availability of high-frequency financial data; see Andersen, Bollerslev, Diebold, and Labys (2001a, 2001b).
Suppose that we are interested in the monthly volatility of an asset for which daily returns are available. Let 
be the monthly log return of the asset at month t. Assume that there are n trading days in month t and the daily log returns of the asset in the month are 
. Using properties of log returns, we have
Assuming that the conditional variance and covariance exist, we have
where Ft−1 denotes the information available at month t − 1 (inclusive). The prior equation can be simplified if additional assumptions are made. For example, if we assume that {rt, i} is a white noise series, then
where Var(rt, 1) can be estimated from the daily returns 
by
where 
is the sample mean of the daily log returns in month t [i.e., 
]. The estimated monthly volatility is then
If {rt, i} follows an MA(1) model, then
which can be estimated by
The previous approach for volatility estimation is simple, but it encounters several difficulties in practice. First, the model for daily returns {rt, i} is unknown. This complicates the estimation of covariances in Eq. (3.48). Second, there are roughly 21 trading days in a month, resulting in a small sample size. The accuracy of the estimates of variance and covariance in Eq. (3.48) might be questionable. The accuracy depends on the dynamic structure of {rt, i} and their distribution. If the daily log returns have high excess kurtosis and serial correlations, then the sample estimates 
in Eqs. (3.49) and (3.50) may not even be consistent; see Bai, Russell, and Tiao (2004). Further research is needed to make this approach valuable.
Example 3.6
Consider the monthly volatility of the log returns of the S&P 500 index from January 1980 to December 1999. We calculate the volatility by three methods. In the first method, we use daily log returns and Eq. (3.49) (i.e., assuming that the daily log returns form a white noise series). The second method also uses daily returns but assumes an MA(1) model [i.e., using Eq. (3.50)]. The third method applies a GARCH(1,1) model to the monthly returns from January 1962 to December 1999. We use a longer data span to obtain a more accurate estimate of the monthly volatility. The GARCH(1,1) model used is
where ϵt is a standard Gaussian white noise series. Figure 3.12 shows the time plots of the estimated monthly volatility. Clearly the estimated volatilities based on daily returns are much higher than those based on monthly returns and a GARCH(1,1) model. In particular, the estimated volatility for October 1987 was about 680 when daily returns are used. The plots shown were truncated to have the same scale.
Figure 3.12 Time plots of estimated monthly volatility for log returns of S&P 500 index from January 1980 to December 1999: (a) assumes that daily log returns form a white noise series, (b) assumes that daily log returns follow an MA(1) model, and (c) uses monthly returns from January 1962 to December 1999 and a GARCH(1,1) model.
In Eq. (3.49), if we further assume that the sample mean 
t is zero, then we have 
. In this case, the cumulative sum of squares of daily log returns in a month is used as an estimate of monthly volatility. This concept has been generalized to estimate daily volatility of an asset by using intradaily log returns. Let rt be the daily log return of an asset. Suppose that there are n equally spaced intradaily log returns available such that 
. The quantity
is called the realized volatility of rt; see Andersen et al. (2001a,b). Mathematically, realized volatility is a quadratic variation of rt, and it assumes that 
forms an iid sequence with mean zero and finite variance. Limited experience indicates that ln(RVt) often follows approximately a Gaussian ARIMA(0,1,q) model, which can be used to produce forecasts. See demonstration in Section 11.1 for further information.
Advantages of realized volatility include simplicity and making use of intradaily returns. Intuitively, one would like to use as much information as possible by choosing a large n. However, when the time interval between rt, i is small, the returns are subject to the effects of market microstructure, for example, bid–ask bounce, which often results in a biased estimate of the volatility. The problem of choosing an optimal time interval for constructing realized volatility has attracted much research lately. For heavily traded assets in the United States, a time interval of 4–15 minutes is often used. Another problem of using realized volatility for stock returns is that the overnight return, which is the return from the closing price of day t − 1 to the opening price of t, tends to be substantial. Ignoring overnight returns can seriously underestimate the volatility. On the other hand, our limited experience shows that overnight returns appear to be small for index returns or foreign exchange returns.
In a series of recent articles, Barndorff-Nielsen and Shephard (2004) have used high-frequency returns to study bi-power variations of an asset return and developed some methods to detect jumps in volatility.
3.15.2 Use of Daily Open, High, Low, and Close Prices
For many assets, daily opening, high, low, and closing prices are available. Parkinson (1980), Garman and Klass (1980), Rogers and Satchell (1991), and Yang and Zhang (2000) showed that one can use such information to improve volatility estimation. Figure 3.13 shows a time plot of price versus time for the tth trading day, assuming that time is continuous. For an asset, define the following variables:
- Ct = closing price of the tth trading day.
- Ot = opening price of the tth trading day.
- f = fraction of the day (in interval [0,1]) that trading is closed.
- Ht = highest price of the tth trading period.
- Lt = lowest price of the tth trading period.
- Ft−1 = public information available at time t − 1.
Figure 3.13 Time plot of price over time: scale for price is arbitrary.
The conventional variance (or volatility) is 
. Garman and Klass (1980) considered several estimates of 
assuming that the price follows a simple diffusion model without drift; see Chapter 6 for more information about stochastic diffusion models. The estimators considered include:
.
.
.
.
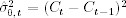, which is ≈ 0.5(Ht − Lt)2 − 0.386(Ct − Ot)2.
.
A more precise, but complicated, estimator 
was also considered. However, it is close to 
. Defining the efficiency factor of a volatility estimator as
Garman and Klass (1980) found that Eff(
) is approximately 2, 5.2, 6.2, 7.4, and 8.4 for i = 1, 2, 3, 5, and 6, respectively, for the simple diffusion model entertained. Note that 
was derived by Parkinson (1980) with f = 0.
Turn to log returns. Define the following:
- ot = ln(Ot) − ln(Ct−1), the normalized open.
- ut = ln(Ht) − ln(Ot), the normalized high.
- dt = ln(Lt) − ln(Ot), the normalized low.
- ct = ln(Ct) − ln(Ot), the normalized close.
Suppose that there are n days of data available and the volatility is constant over the period. Yang and Zhang (2000) recommend the estimate
as a robust estimator of the volatility, where
The estimate 
was proposed by Rogers and Satchell (1991), and the quantity k is chosen to minimize the variance of the estimator of 
, which is a linear combination of three estimates.
The quantity Ht − Lt is called the range of the price in the tth day. This estimator has led to the use of range-based volatility estimates; see, for instance, Alizadeh, Brandt, and Diebold (2002). In practice, stock prices are only observed at discrete time points. As such, the observed daily high is likely lower than Ht and the observed daily low is likely higher than Lt. Consequently, the observed daily price range tends to underestimate the actual range and, hence, may lead to underestimation of volatility. This bias in volatility estimation depends on the trading frequency and tick size of the stocks. For intensively traded stocks, the bias should be negligible. For other stocks, further study is needed to better understand the performance of range-based volatility estimation.