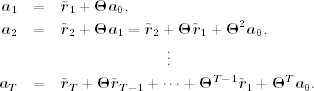8.3 Vector Moving-Average Models
A vector moving-average model of order q, or VMA(q), is in the form
where 
is a k-dimensional vector, 
are k × k matrices, and 
is the MA matrix polynomial in the back-shift operator B. Similar to the univariate case, VMA(q) processes are weakly stationary provided that the covariance matrix 
of 
exists. Taking expectation of Eq. (8.23), we obtain that 
. Thus, the constant vector 
is the mean vector of 
for a VMA model.
Let 
be the mean-corrected VAR(q) process. Then using Eq. (8.23) and the fact that 
has no serial correlations, we have
1. Cov(
) = 
.
2. 
.
3. 
if ℓ > q.
4. 
if 1 ≤ ℓ ≤ q, where 
.
Since 
for ℓ > q, the cross-correlation matrices (CCMs) of a VMA(q) process 
satisfy
8.24 
Therefore, similar to the univariate case, the sample CCMs can be used to identify the order of a VMA process.
To better understand the VMA processes, let us consider the bivariate MA(1) model
where, for simplicity, the subscript of 
is removed. This model can be written explicitly as
8.26 
It says that the current return series 
only depends on the current and past shocks. Therefore, the model is a finite-memory model.
Consider the equation for r1t in Eq. (8.27). The parameter Θ12 denotes the linear dependence of r1t on a2, t−1 in the presence of a1, t−1. If Θ12 = 0, then r1t does not depend on the lagged values of a2t and, hence, the lagged values of r2t. Similarly, if Θ21 = 0, then r2t does not depend on the past values of r1t. The off-diagonal elements of 
thus show the dynamic dependence between the component series. For this simple VMA(1) model, we can classify the relationships between r1t and r2t as follows:
1. They are uncoupled series if Θ12 = Θ21 = 0.
2. There is a unidirectional dynamic relationship from r1t to r2t if 
= 0, but Θ21 ≠ 0. The opposite unidirectional relationship holds if Θ21 = 0, but Θ12 ≠ 0.
3. There is a feedback relationship between r1t and r2t if Θ12 ≠ 0 and Θ21 ≠ 0.
Finally, the concurrent correlation between rit is the same as that between ait. The previous classification can be generalized to a VMA(q) model.
Estimation
Unlike the VAR models, estimation of VMA models is much more involved; see Hillmer and Tiao (1979), Lütkepohl (2005), and the references therein. For the likelihood approach, there are two methods available. The first is the conditional-likelihood method that assumes that 
for t ≤ 0. The second is the exact-likelihood method that treats 
with t ≤ 0 as additional parameters of the model. To gain some insight into the problem of estimation, we consider the VMA(1) model in Eq. (8.25). Suppose that the data are 
and 
is multivariate normal. For a VMA(1) model, the data depend on 
.
8.3.1.1 Conditional MLE
The conditional-likelihood method assumes that 
= 
. Under such an assumption and rewriting the model as 
, we can compute the shock 
recursively as
Consequently, the likelihood function of the data becomes
which can be evaluated to obtain the parameter estimates.
8.3.1.2 Exact MLE
For the exact-likelihood method, 
is an unknown vector that must be estimated from the data to evaluate the likelihood function. For simplicity, let 
be the mean-corrected series. Using 
and Eq. (8.25), we have
By repeated substitutions, 
is related to all 
as
Thus, 
is a linear function of the data if 
and 
are given. This result enables us to estimate 
using the data and initial estimates of 
and 
. More specifically, given 
, 
, and the data, we can define
Equation (8.29) can then be rewritten as
This is in the form of a multiple linear regression with parameter vector 
, even though the covariance matrix 
of 
may not be a diagonal matrix. If initial estimate of 
is also available, one can premultiply each equation of the prior system by 
, which is the square root matrix of 
. The resulting system is indeed a multiple linear regression, and the ordinary least-squares method can be used to obtain an estimate of 
. Denote the estimate by 
.
Using the estimate 
, we can compute the shocks 
recursively as
This recursion is a linear transformation from 
to 
, from which we can (a) obtain the joint distribution of 
and the data, and (2) integrate out 
to derive the exact-likelihood function of the data. The resulting likelihood function can then be evaluated to obtain the exact ML estimates. For details, see Hillmer and Tiao (1979).
In summary, the exact-likelihood method works as follows. Given initial estimates of 
, 
, and 
, one uses Eq. (8.29) to derive an estimate of 
. This estimate is in turn used to compute 
recursively using Eq. (8.28) and starting with 
. The resulting 
are then used to evaluate the exact-likelihood function of the data to update the estimates of 
, 
, and 
. The whole process is then repeated until the estimates converge. This iterative method to evaluate the exact-likelihood function applies to the general VMA(q) models.
From the previous discussion, the exact-likelihood method requires more intensive computation than the conditional-likelihood approach does. But it provides more accurate parameter estimates, especially when some eigenvalues of 
are close to 1 in modulus. Hillmer and Tiao (1979) provide some comparison between the conditional- and exact-likelihood estimations of VMA models. In multivariate time series analysis, the exact maximum-likelihood method becomes important if one suspects that the data might have been overdifferenced. Overdifferencing may occur in many situations (e.g., differencing individual components of a cointegrated system; see discussion later on cointegration).
In summary, building a VMA model involves three steps: (a) Use the sample cross-correlation matrices to specify the order q—for a VMA(q) model, 
for ℓ > q; (b) estimate the specified model by using either the conditional- or exact-likelihood method—the exact method is preferred when the sample size is not large; and (c) the fitted model should be checked for adequacy [e.g., applying the Qk(m) statistics to the residual series]. Finally, forecasts of a VMA model can be obtained by using the same procedure as a univariate MA model.
Example 8.5
Consider again the bivariate series of monthly log returns in percentages of IBM stock and the S&P 500 index from January 1926 to December 2008. Since significant cross correlations occur mainly at lags 1, 2, 3 and 5, we employ the VMA(5) model
for the data. Table 8.6 shows the estimation results of the model. The Qk(m) statistics for the residuals of the simplified model give Q2(4) = 16.00 and Q2(8) = 29.46. Compared with chi-squared distributions with 10 and 26 degrees of freedom, the p values of these statistics are 0.10 and 0.291, respectively. Thus, the model is adequate at the 5% significance level.
From Table 8.6, we make the following observations:
1. The difference between conditional- and exact-likelihood estimates is small for this particular example. This is not surprising because the sample size is not small and, more important, the dynamic structure of the data is weak.
2. The VMA(5) model provides essentially the same dynamic relationship for the series as that of the VAR(5) model in Example 8.4. The monthly log return of IBM stock depends on the previous returns of the S&P 500 index. The market return, in contrast, does not depend on lagged returns of IBM stock. In other words, the dynamic structure of the data is driven by the market return, not by the IBM return. The concurrent correlation between the two returns remains strong, however.
Table 8.6 Estimation Results for Monthly Log Returns of IBM Stock and S&P 500 Index Using the Vector Moving-Average Model in Eq. (8.30)a
aThe sample period is from January 1926 to December 2008. The residual covariance matrix is not shown as it is similar to that in Table 8.4