Now, we will compute the gradients of loss with respect to hidden to hidden layer weights, . Similar to , the final gradient is the sum of the gradients at all time steps:

So, we can write:

First, let's compute gradient of loss, with respect to , that is, .

We cannot compute derivative of with respect to directly from as there are no terms in it. So, we use the chain rule to compute the gradients of loss with respect to . Let's recollect the forward propagation equation:

First, we calculate the partial derivative of loss with respect to ; then, from , we calculate the partial derivative with respect to ; then, from , we can calculate the derivative with respect to W, as follows:

Now, let's compute the gradient of loss, with respect to , that is, 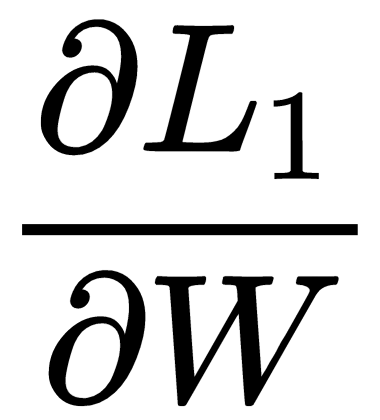. Thus, again, we will apply the chain rule and get the following:

If you look at the preceding equation, how can we calculate the term ? Let's recall the equation of :

As you can see in the preceding equation, computing depends on and , but is not a constant; it is a function again. So, we need to calculate the derivative with respect to that, as well.

The equation then becomes the following:

The following figure shows computing ; we can notice how is dependent on :

Now, let's compute the gradient of loss, with respect to , that is,. Thus, again, we will apply the chain rule and get the following:

In the preceding equation, we can't compute directly. Recall the equation of :

As you observe, computing , depends on a function , whereas is again a function which depends on function . As shown in the following figure, to compute the derivative with respect to , we need to traverse until , as each function is dependent on one another:

This can be pictorially represented as follows:

This applies for the loss at any time step; say, . So, we can say that to compute any loss , we need to traverse all the way to , as shown in the following figure:

This is because in RNNs, the hidden state at a time is dependent on a hidden state at a time 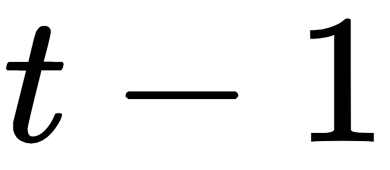, which implies that the current hidden state is always dependent on the previous hidden state.

So, any loss can be computed as shown in the following figure:

Thus, we can write, gradient of loss with respect to becomes:

The sum in the previous equation implies the sum over all the hidden states . In the preceding equation, can be computed using the chain rule. So, we can say:

Assume that j=3 and k=0; then, the preceding equation becomes:

Substituting equation (12) into equation (11) will give us the following:

We know that final loss is the sum of loss across all the time steps:

Substituting equation (13) into the preceding equation, we get the following:

We have two summations in the preceding equation, where:

• implies the sum of loss across all the time steps
• is the summation over hidden states

So, our final equation for computing gradient of loss with respect to W, is given as:

Now, we will look at how to compute each of the terms in the preceding equation, one by one. From equation (4) and equation (9), we can say that:

Let's look at the next term:

We know that the hidden state is computed as:

The derivative of 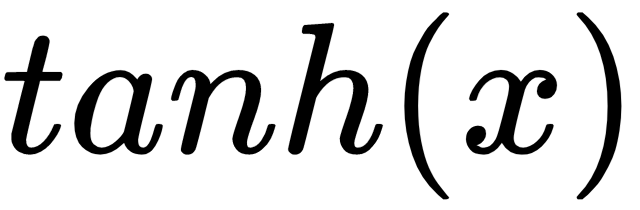is , so we can write:

Let's look at the final term . We know that the hidden state is computed as, . Thus, the derivation of with respect to becomes:

Substituting all of the calculated terms into equation (15), we get our final equation for gradient of loss 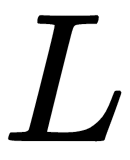with respect to as follows: