Adadelta is an enhancement of the Adagrad algorithm. In Adagrad, we noticed the problem of the learning rate diminishing to a very low number. Although Adagrad learns the learning rate adaptively, we still need to set the initial learning rate manually. However, in Adadelta, we don't need the learning rate at all. So how does the Adadelta algorithm learn?

In Adadelta, instead of taking the sum of all the squared past gradients, we can set a window of size and take the sum of squared past gradients only from that window. In Adagrad, we took the sum of all the squared past gradients and it led to the learning rate diminishing to a low number. To avoid that, we take the sum of the squared past gradients only from a window.

If is the window size, then our parameter update equation becomes the following:

However, the problem is that, although we are taking gradients only from within a window, , squaring and storing all the gradients from the window in each iteration is inefficient. So, instead of doing that, we can take the running average of gradients.

We compute the running average of gradients at an iteration, t, , by adding the previous running average of gradients, , and current gradients, :

Instead of just taking the running average, we take the exponentially decaying running average of gradients, as follows:

Here, is called the exponential decaying rate and is similar to the one we saw in momentum – that is, it is used for deciding how much information from the previous running average of gradients should be added.

Now, our update equation becomes the following:

For notation simplicity, let's denote as so that we can rewrite the previous update equation as follows:

From the previous equation, we can infer the following:

If you look at the denominator in the previous equation, we are basically computing the root mean squared of gradients up to an iteration, , so we can simply write that in shorthand as follows:

By substituting equation (13) in equation (12), we can write the following:

However, we still have the learning rate, , term in our equation. How can we do away with that? We can do so by making the units of the parameter update in accordance with the parameter. As you may have noticed, the units of and don't really match. To combat this, we compute the exponentially decaying average of the parameter updates,, as we computed an exponentially decaying average of gradients, , in equation (10). So, we can write the following:

It's like the RMS of gradients, , which is similar to equation (13). We can write the RMS of the parameter update as follows:

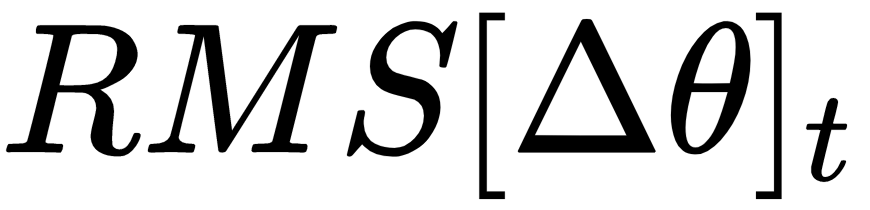However, the RMS value for the parameter update, is not known, that is, is not known, so we can just approximate it by considering until the previous update, .

Now, we just replace our learning rate with the RMS value of the parameter updates. That is, we replace with in equation (14) and write the following:

Substituting equation (15) in equation (11), our final update equation becomes the following:

Now, let's understand the Adadelta algorithm by implementing it.

First, we define the AdaDelta function:

def AdaDelta(data, theta, gamma = 0.9, epsilon = 1e-5, num_iterations = 1000):

Then, we initialize the E_grad2 variable with zero for storing the running average of gradients, and E_delta_theta2 with zero for storing the running average of the parameter update, as follows:

    # running average of gradients
    E_grad2 = np.zeros(theta.shape[0])

    #running average of parameter update
    E_delta_theta2 = np.zeros(theta.shape[0])

For every iteration, we perform the following steps:

    for t in range(num_iterations):

Now, we need to compute the gradients with respect to theta:

        gradients = compute_gradients(data, theta) 

Then, we can compute the running average of gradients:

        E_grad2 = (gamma * E_grad2) + ((1. - gamma) * (gradients ** 2))

Here, we will compute delta_theta, that is, :

        delta_theta = - (np.sqrt(E_delta_theta2 + epsilon)) / (np.sqrt(E_grad2 + epsilon)) * gradients

Now, we can compute the running average of the parameter update, :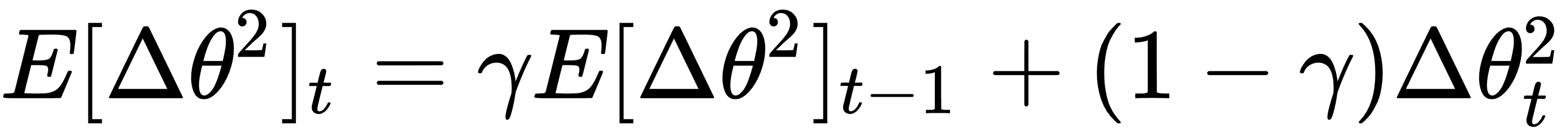

        E_delta_theta2 = (gamma * E_delta_theta2) + ((1. - gamma) * (delta_theta ** 2))

Next, we will update the parameter of the model, theta, so that it's :

        theta = theta + delta_theta

    return theta