If the cost or loss is very high, then it means that our network is not predicting the correct output. So, our objective is to minimize the cost function so that our neural network predictions will be better. How can we minimize the cost function? That is, how can we minimize the loss/cost? We learned that the neural network makes predictions using forward propagation. So, if we can change some values in the forward propagation, we can predict the correct output and minimize the loss. But what values can we change in the forward propagation? Obviously, we can't change input and output. We are now left with weights and bias values. Remember that we just initialized weight matrices randomly. Since the weights are random, they are not going to be perfect. Now, we will update these weight matrices ( and ) in such a way that our neural network gives a correct output. How do we update these weight matrices? Here comes a new technique called gradient descent.

With gradient descent, the neural network learns the optimal values of the randomly initialized weight matrices. With the optimal values of weights, our network can predict the correct output and minimize the loss.

Now, we will explore how the optimal values of weights are learned using gradient descent. Gradient descent is one of the most commonly used optimization algorithms. It is used for minimizing the cost function, which allows us to minimize the error and obtain the lowest possible error value. But how does gradient descent find the optimal weights? Let's begin with an analogy.

Imagine we are on top of a hill, as shown in the following diagram, and we want to reach the lowest point on the hill. There could be many regions that look like the lowest points on the hill, but we have to reach the lowest point that is actually the lowest of all.

That is, we should not be stuck at a point believing it is the lowest point when the global lowest point exists:

Similarly, we can represent our cost function as follows. It is a plot of cost against weights. Our objective is to minimize the cost function. That is, we have to reach the lowest point where the cost is the minimum. The solid dark point in the following diagram shows the randomly initialized weights. If we move this point downward, then we can reach the point where the cost is the minimum:

But how can we move this point (initial weight) downward? How can we descend and reach the lowest point? Gradients are used for moving from one point to another. So, we can move this point (initial weight) by calculating a gradient of the cost function with respect to that point (initial weights), which is .

Gradients are the derivatives that are actually the slope of a tangent line as illustrated in the following diagram. So, by calculating the gradient, we descend (move downward) and reach the lowest point where the cost is the minimum. Gradient descent is a first-order optimization algorithm, which means we only take into account the first derivative when performing the updates:

Thus, with gradient descent, we move our weights to a position where the cost is minimum. But, still, how do we update the weights?

As a result of forward propagation, we are in the output layer. We will now backpropagate the network from the output layer to the input layer and calculate the gradient of the cost function with respect to all the weights between the output and the input layer so that we can minimize the error. After calculating gradients, we update our old weights using the weight update rule:

This implies weights = weights -α * gradients.

What is ? It is called the learning rate. As shown in the following diagram, if the learning rate is small, then we take a small step downward and our gradient descent can be slow.

If the learning rate is large, then we take a large step and our gradient descent will be fast, but we might fail to reach the global minimum and become stuck at a local minimum. So, the learning rate should be chosen optimally:

This whole process of backpropagating the network from the output layer to the input layer and updating the weights of the network using gradient descent to minimize the loss is called backpropagation. Now that we have a basic understanding of backpropagation, we will strengthen our understanding by learning about this in detail, step-by-step. We are going to look at some interesting math, so put on your calculus hats and follow the steps.

So, we have two weights, one ,input to hidden layer weights, and the other , hidden to output layer weights. We need to find the optimal values for these two weights that will give us the fewest errors. So, we need to calculate the derivative of the cost function with respect to these weights. Since we are backpropagating, that is, going from the output layer to the input layer, our first weight will be. So, now we need to calculate the derivative of with respect to . How do we calculate the derivative? First, let's recall our cost function, :

We cannot calculate the derivative directly from the preceding equation since there is no

term. So, instead of calculating the derivative directly, we calculate the partial derivative. Let's recall our forward propagation equation:

First, we will calculate a partial derivative with respect to , and then from we will calculate the partial derivative with respect to . From , we can directly calculate our derivative . It is basically the chain rule. So, the derivative of with respect to becomes as follows:

Now, we will compute each of the terms in the preceding equation:

Here, 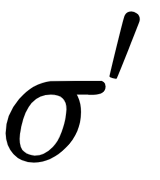is the derivative of our sigmoid activation function. We know that the sigmoid function is , so the derivative of the sigmoid function would be :

Thus, substituting all the preceding terms in equation (1) we can write:

Now we need to compute a derivative of with respect to our next weight,.

Similarly, we cannot calculate the derivative of directly from as we don't have any terms in . So, we need to use the chain rule. Let's recall the forward propagation steps again:

Now, according to the chain rule, the derivative of with respect to is given as:

We have already seen how to compute the first terms in the preceding equation; now, we will see how to compute the rest of the terms:

Thus, substituting all the preceding terms in equation (3) we can write:

After we have computed gradients for both weights, and , we will update our initial weights according to the weight update rule:

That's it! This is how we update the weights of a network and minimize the loss. If you don't understand gradient descent yet, no worries! In Chapter 3, Gradient Descent and Its Variants, we will go into the basics and learn gradient descent and several variants of gradient descent in more detail. Now, let's see how to implement the backpropagation algorithm in Python.

In both the equations (2) and (4), we have the term 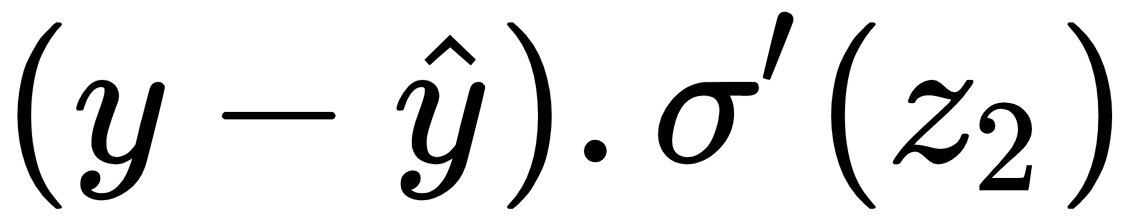, so instead of computing them again and again, we just call them delta2:

delta2 = np.multiply(-(y-yHat),sigmoidPrime(z2))

Now, we compute the gradient with respect to . Refer to equation (2):

dJ_dWhy = np.dot(a1.T,delta2)

We compute the gradient with respect to . Refer to equation (4):

delta1 = np.dot(delta2,Why.T)*sigmoidPrime(z1)

dJ_dWxh = np.dot(X.T,delta1)

We will update the weights according to our weight update rule equation (5) and (6) as follows:

Wxh = Wxh - alpha * dJ_dWhy
Why = Why - alpha * dJ_dWxh 

The complete code for the backpropagation is given as follows:

def backword_prop(y_hat, z1, a1, z2):
    delta2 = np.multiply(-(y-y_hat),sigmoid_derivative(z2))
    dJ_dWhy = np.dot(a1.T, delta2)

    delta1 = np.dot(delta2,Why.T)*sigmoid_derivative(z1)
    dJ_dWxh = np.dot(X.T, delta1) 

    Wxh = Wxh - alpha * dJ_dWhy
    Why = Why - alpha * dJ_dWxh


    return Wxh,Why

Before moving on, let's familiarize ourselves with some of the frequently used terminologies in neural networks:

• Forward pass: Forward pass implies forward propagating from the input layer to the output layer.
• Backward pass: Backward pass implies backpropagating from the output layer to the input layer.
• Epoch: The epoch specifies the number of times the neural network sees our whole training data. So, we can say one epoch is equal to one forward pass and one backward pass for all training samples.
• Batch size: The batch size specifies the number of training samples we use in one forward pass and one backward pass.
• Number of iterations: The number of iterations implies the number of passes where one pass = one forward pass + one backward pass.

Say that we have 12,000 training samples and that our batch size is 6,000. It will take us two iterations to complete one epoch. That is, in the first iteration, we pass the first 6,000 samples and perform a forward pass and a backward pass; in the second iteration, we pass the next 6,000 samples and perform a forward pass and a backward pass. After two iterations, our neural network will see the whole 12,000 training samples, which makes it one epoch.