Once we have predicted the output, we compute the loss, 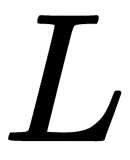. We use the mean squared error as the loss function, that is, the mean of the squared difference between the actual output, , and the predicted output, , which is given as follows:

Now, we will see how can we use backpropagation to minimize the loss . In order to minimize the loss, we need to find the optimal values for our filter W. Our filter matrix consists of four values, w1, w2, w3, and w4. To find the optimal filter matrix, we need to calculate the gradients of our loss function with respect to all these four values. How do we do that?

First, let's recollect the equations of the output matrix, as follows:

Don't get intimidated by the upcoming equations; they are actually pretty simple.

First, let's calculate gradients with respect to . As you can see,  appears in all the output equations; we calculate the partial derivatives of the loss with respect to  as follows:

Similarly, we calculate the partial derivative of the loss with respect to the weight as follows:

The gradients of loss with respect to the weights, are calculated as follows:

The gradients of loss with respect to the weights, are given as follows:

So, in a nutshell, our final equations for the gradients of loss with respect to all the weights are as follows:

It turns out that computing the derivatives of loss with respect to the filter matrix is very simple—it is just another convolution operation. If we look at the preceding equations closely, we will notice they look like the result of a convolution operation between the input matrix and the gradient of the loss with respect to the output as a filter matrix, as depicted in the following diagram:

For example, let's see how the gradients of loss with respect to weight are computed by the convolution operation between the input matrix and the gradients of loss with respect to the output as a filter matrix, as shown in the following diagram:

Thus, we can write the following:

So, we understand that computing the gradients of loss with respect to the filter (that is, weights) is just the convolution operation between the input matrix and the gradient of loss with respect to the output as a filter matrix.

Apart from calculating the gradients of loss with respect to the filter, we also need to calculate the gradients of loss with respect to an input. But why do we do that? Because it is used for calculating the gradients of the filters present in the previous layer.

Our input matrix consists of nine values, from to , so we need to calculate the gradients of loss with respect to all these nine values. Let's recollect how the output matrix is computed:

As you can see, is present only in , so we can calculate the gradients of loss with respect to alone, as other terms would be zero:

Now, let's calculate the gradients with respect to 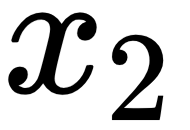; as 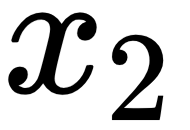is present in only and , we calculate the gradients with respect to and alone:

In a very similar way, we calculate the gradients of loss with respect to all the inputs as follows:

Just as we represented the gradients of the loss with respect to the weights using the convolution operation, can we also do the same here? It turns out that the answer is yes. We can actually represent the preceding equations, that is, the gradients of loss with respect to the inputs, using a convolution operation between the filter matrix as an input matrix and the gradients of loss with respect to the output matrix as a filter matrix. But the trick is that, instead of using the filter matrix directly, we rotate them 180 degrees and, also, instead of performing convolution, we perform full convolution. We are doing this so that we can derive the previous equations using a convolution operation.

The following shows what the kernel rotated by 180 degrees looks like:

Okay, so what is full convolution? In the same way as a convolution operation, in full convolution, we use a filter and slide it over the input matrix, but the way we slide the filter is different from the convolution operation we looked at before. The following figure shows how full convolution operations work. As we can see, the shaded matrix represents the filter matrix and the unshaded one represents the input matrix; we can see how the filter slides over the input matrix step by step, as shown in this diagram:

So, we can say that the gradient of loss with respect to the input matrix can be calculated using a full convolution operation between a filter rotated by 180 degrees as the input matrix and the gradient of the loss with respect to the output as a filter matrix:

For example, as shown in the following figure, we will notice how the gradients of loss with respect to the input, , is computed by the full convolution operation between the filter matrix rotated by 180 degrees, and the gradients of loss with respect to an output matrix as a filter matrix:

This is demonstrated as follows:

Thus, we understand that computing the gradients of loss with respect to the input is just the full convolution operation. So, we can say that backpropagation in CNN is just another convolution operation.