Before we get into the details, let's understand the basics. What is a function in mathematics? A function represents the relation between input and output. We generally use to denote a function. For instance, implies a function that takes as an input and returns as an output. It can also be represented as .

Here, we have a function, , and we can plot and see what our function looks like:

The smallest value of a function is called the minimum of a function. As you can see in the preceding plot, the minimum of the function lies at 0. The previous function is called a convex function, and is where we have only one minimum value. A function is called a non-convex function when there is more than one minimum value. As we can see in the following diagram, a non-convex function can have many local minima and one global minimum value, whereas a convex function has only one global minimum value:

By looking at the graph of the function, we can easily say that it has its minimum value at . But how can we find the minimum value of a function mathematically? First, let's assume x = 0.7. Thus, we are at a position where x = 0.7, as shown in the following graph:

Now, we need to go to zero, which is our minimum value, but how can we reach it? We can reach it by calculating the derivative of the function, . So, the derivative of the function, , with respect to , is as follows:

Since we are at x = 0.7 and substituting this in the previous equation, we get the following equation:

After calculating the derivative, we update our position of according to the following update rule:

As we can see in the following graph, we were at x = 0.7 initially, but, after computing the gradient, we are now at the updated position of x = -0.7. However, this is something we don't want because we missed our minimum value, which is x = 0, and reached somewhere else:

To avoid this, we introduce a new parameter called learning rate, , in the update rule. It helps us to slow down our gradient steps so that we won't miss out the minimal point. We multiply the gradients by the learning rate and update the value, as follows:

Let's say that ; now, we can write the following:

As we can see in the following graph, after multiplying the gradients by the learning rate with the updated x value, we descended from the initial position, x = 0.7, to x = 0.49:

However, this still isn't our optimal minimum value. We need to go further down until we reach the minimum value; that is, x = 0. So, for some n number of iterations, we have to repeat the same process until we reach the minimal point. That is, for some n number of iterations, we update the value of x using the following update rule until we reach the minimal point:

Okay – why is there a minus in the preceding equation? That is, why we are subtracting from x? Why can't we add them and have our equation as ?

This is because we are finding the minimum of a function, so we need to go downward. If we add x to , then we go upward on every iteration, and we cannot find the minimum value, as shown in the following graphs:

Thus, on every iteration, we compute gradients of y with respect to x, that is, , multiply the gradients by the learning rate, that is, , and subtract it from the x value to get the updated x value, as follows:

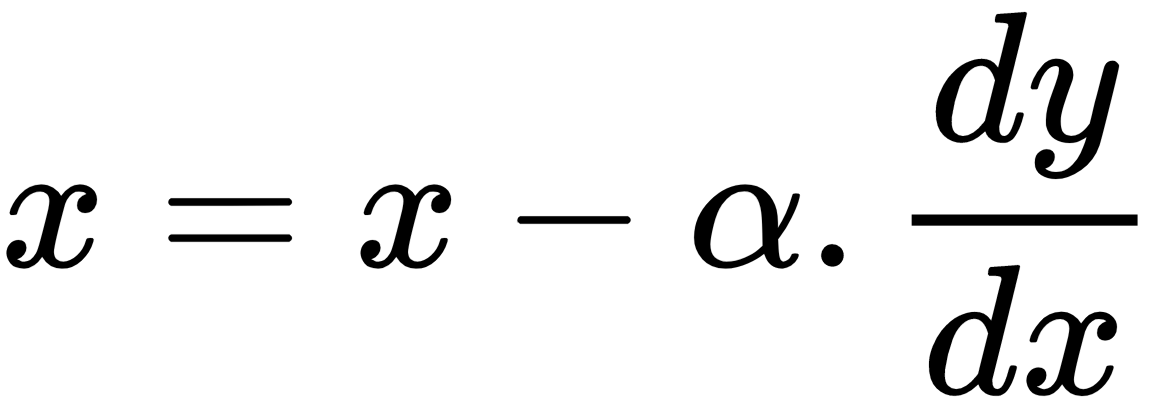
By repeating this step on every iteration, we go downward from the cost function and reach the minimum point. As we can see in the following graph, we moved downward from the initial position of 0.7 to 0.49, and then, from there, we reached 0.2.

Then, after several iterations, we reach the minimum point, which is 0.0:

We say we attained convergence when we reach the minimum of the function. But the question is: how do we know that we attained convergence? In our example, , we know that the minimum value is 0. So, when we reach 0, we can say that we found the minimum value that we attained convergence. But how can we mathematically say that 0 is the minimum value of the function, ?

Let's take a closer look at the following graph, which shows how the value of x changes on every iteration. As you may notice, the value of x is 0.009 in the fifth iteration, 0.008 in the sixth iteration, and 0.007 in the seventh iteration. As you can see, there's not much difference between the fifth, sixth, and seventh iterations. When there is little change in the value of x over iterations, then we can conclude that we have attained convergence:

Okay, but what is the use of all this? Why are we trying to find the minimum of a function? When we're training a model, our goal is to minimize the loss function of the model. Thus, with gradient descent, we can find the minimum of the cost function. Finding the minimum of the cost function gives us an optimal parameter of the model with which we can obtain the minimal loss. In general, we denote the parameters of the model by . The following equation is called the parameter update rule or weight update rule:

Here, we have the following:

• is the parameter of the model
• is the learning rate
• is the gradient

We update the parameter of the model for several iterations according to the parameter update rule until we attain convergence.