When we build a deep neural network, we have many parameters. Parameters are basically the weights of the network, so when we build a network with many layers, we will have many weights, say, . Our goal is to find the optimal values for all these weights. In all of the previous methods we learned about, the learning rate was a common value for all the parameters of the network. However Adagrad (short for adaptive gradient) adaptively sets the learning rate according to a parameter.

Parameters that have frequent updates or high gradients will have a slower learning rate, while a parameter that has an infrequent update or small gradients will also have a slower learning rate. But why do we have to do this? It is because parameters that have infrequent updates implies that they are not trained enough, so we set a high learning rate for them, and parameters that have frequent updates implies that they are trained enough, so we set their learning rate to a low value so that we don't overshoot the minimum.

Now, let's see how Adagrad adaptively changes the learning rate. Previously, we represented the gradient with . For simplicity, from now on in this chapter, we'll represent gradients with . So, the gradient of a parameter, , at an iteration, , can be represented as follows:

Therefore, we can rewrite our update equation with as the gradient notation as follows:

Now, for every iteration, , to update a parameter, , we divide the learning rate by the sum of squares of all previous gradients of the parameter, , as follows:

Here, implies the sum of squares of all previous gradients of the parameter . We added just to avoid the division by zero error. We typically set the value of to a small number. The question that arises here is, why are we dividing the learning rate by a sum of squares of all the previous gradients?

We learned that parameters that have frequent updates or high gradients will have a slower learning rate, while parameters that have an infrequent update or small gradients will also have a high learning rate.

The sum,, actually scales our learning rate. That is, when the sum of the squared past gradients has a high value, we are basically dividing the learning rate by a high value, so our learning rate will become less. Similarly, if the sum of the squared past gradients has a low value, we are dividing the learning rate by a lower value, so our learning rate value will become high. This implies that the learning rate is inversely proportional to the sum of the squares of all the previous gradients of the parameter.

Here, our update equation is expressed as follows:

In a nutshell, in Adagrad, we set the learning rate to a low value when the previous gradient value is high, and to a high value when the past gradient value is lower. This means that our learning rate value changes according to the past gradient updates of the parameters.

Now that we have learned how the Adagrad algorithm works, let's strengthen our knowledge by implementing it. The code for the Adagrad algorithm is given as follows.

First, define the AdaGrad function:

def AdaGrad(data, theta, lr = 1e-2, epsilon = 1e-8, num_iterations = 10000):

Define the variable called gradients_sum to hold the sum of gradients and initialize them with zeros:

    gradients_sum = np.zeros(theta.shape[0])

For every iteration, we perform the following steps:

    for t in range(num_iterations):

Then, we compute the gradients of loss with respect to theta:

        gradients = compute_gradients(data, theta) 

Now, we calculate the sum of the gradients squared, that is, :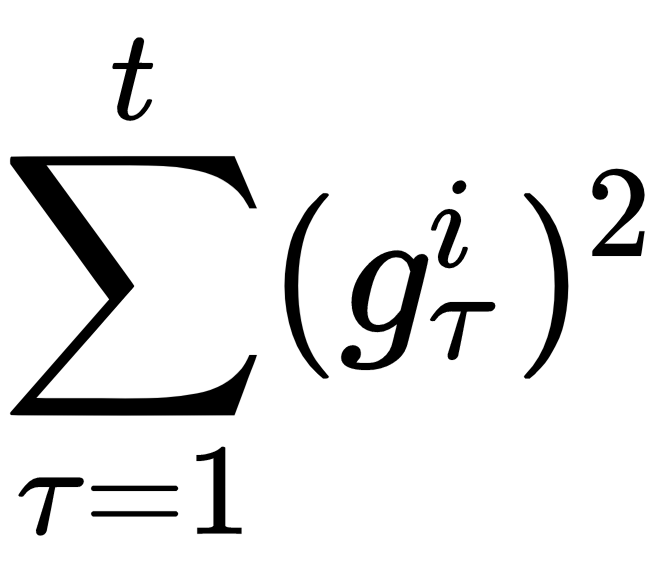

        gradients_sum += gradients ** 2

Afterward, we compute the gradient updates, that is, :

        gradient_update = gradients / (np.sqrt(gradients_sum + epsilon))

Now, update the theta model parameter so that it's :

        theta = theta - (lr * gradient_update)

    return theta

Again, there is a shortcoming associated with the Adagrad method. For every iteration, we are accumulating and summing all the past squared gradients. So, on every iteration, our sum of the squared past gradients value will increase. When the sum of the squared past gradient value is high, we will have a large number in the denominator. When we divide the learning rate by a very large number, then the learning rate will become very small. So, over several iterations, the learning rate starts decaying and becomes an infinitesimally small number – that is, our learning rate will be monotonically decreasing. When the learning rate reaches a very low value, then it takes a long time to attain convergence.

In the next section, we will see how Adadelta tackles this shortcoming.